【時系列データ】ARモデルとMAモデルとARIMAモデルのシミュレーション【R言語と統計の備忘録】

ARIMAモデルに沿った時系列データを、簡単なシミュレーションで確認した際の備忘録です。

特徴をわかりやすくするために、あえて実データではなく、数値データを作成しています。

以下は、時系列分析と状態空間モデルの基礎(著：馬場真哉)を参考にさせて頂いています。

～目次～

1. AR/MA/ARIMAモデルの概要

2. 時系列データを扱う際に使用するパッケージ

3. ARモデルのシミュレーションとコレログラム

4. MAモデルのシミュレーションとコレログラム

5. ARIMAモデルのシミュレーションとコレログラム

6. Rのパッケージを使用したARIMAモデルの作成(arima.sim)

1. AR/MA/ARIMAモデルの概要

AR/MA/ARIMAモデルの概要について。

定常過程と非定常過程

AR/MA/ARIMAモデルは定常過程であることが前提

定常過程には弱定常過程と強定常過程があるが、ARIMAモデルを扱う際は弱定常過程を考慮する

弱定常過程は、簡単に言うと以下の二つを満たす

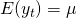$E(y_t)=\mu$ (期待値は時点によらず一定)
自己共分散は時点によらず一定

一つ目は、時間によるトレンドがないことを意味する。
例えば、年々増えていくもの(成長企業の売り上げ)や、減っていく(出生率)などは定常過程ではない。

二つ目は、時点によってトレンドが異なることがないこと。
例えば、去年までは曜日ごとに売り上げの特徴が異なっていたが、今年は月末/月初の影響を受ける、等は定常過程ではない。

ARモデル

ARモデルは自己回帰モデルと呼ばれ、「過去の自分のデータ」を説明変数とする。
・１時点前のデータを使用するモデル式は以下

$y_t = c + a_1y_{t-1}+\epsilon_t$
$c$ :定数項
$a_1$ :係数
$\epsilon_t$ :ホワイトノイズ(平均0、分散 $\sigma^2$ の正規分布)

・n時点前までのデータを使用する一般的なモデル式は以下となり、AR(p)で表す。
(上記の１時点前のデータのみを使用する場合はAR(1))

$y_t = c + \sum_{i=1}^{p}a_iy_{t-i}+\epsilon_t$

なお、上記パラメータにおいて、以下を満たすときARモデルは定常過程ではなくなる。

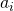$a_i$ の絶対値が1以上(1を含む)時
$c$ の値が0以外の時

一つ目は、1より大きい場合、発散していくため、トレンドができてしまう事が容易に想像がつく

二つ目も同様に、一定の量ずつ増えていけば、期待値 $E(y_t)=\mu$ が上昇する。

なお、二つ目については、和分過程(ARIMAモデルのI)を用いる事で解決できる。
これは、 $y_t-y_{t-1}$ を対象モデルとして扱う事を意味する。
これにより、定数項を消す事ができる。

MAモデル

MAモデルは移動平均モデルと言われる
(為替データなどのテクニカル指標としても有名なものと同じ)

n日の移動平均とは、過去n日の平均値を使う事である。

モデルは以下となり、MA(q)と表記する

$y_t = \mu + \epsilon_t + \sum_{j=1}^{q}\theta_j \epsilon_{t-j}$

$\theta$ は係数で、ある程度自由に設定可能。ただし、以下の条件を満たす必要がある。
※トレンドのある非定常過程になってしまうため

$\sum_{j=1}^{q}\theta_j =0$

MAモデルは、基本的に定常過程である。

ARIMAモデル

ARMAモデルは、単純にARモデルとMAモデルを合わせたモデルである。

$y_t = c + \sum_{i=1}^{n}a_iy_{t-i}+\epsilon_t+ \sum_{j=1}^{n}\theta_j \epsilon_{t-j}$

ARIMAモデルのIは、ARモデルのところでも少し述べた差分を使用する事である。

d回差分をとったモデルはARIMA(p,d,q)と表す。

２. 使用するパッケージ

今回使用しないパッケージも含まれていますが、以下をまとめて入手しておくと便利

install.packages("forecast")
install.packages("tseries")
install.packages("ggplot2")
install.packages("ggfortify")
library(forecast)
library(tseries)
library(ggplot2)
library(ggfortify)

３. ARモデルのシミュレーションとコレログラム

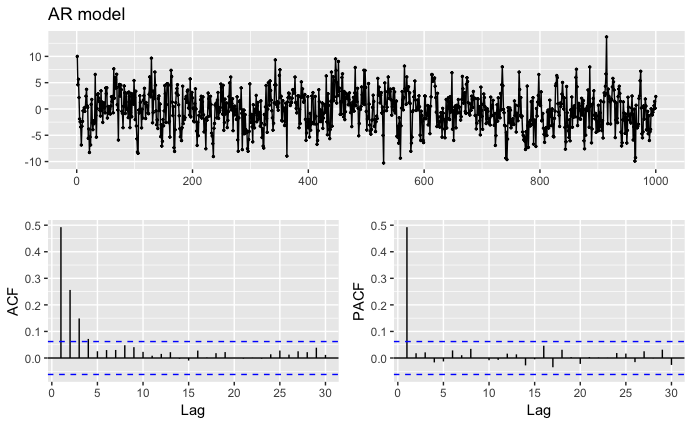
ARモデルは、以下のようにして作成できる。

#p=1で固定
ar = 10 #初期値
fai = 0.5 #係数
for (i in 2:1000){
  ar[i] <- ar[i-1] * fai + rnorm(1,sd=3) #ホワイトノイズは、N(0,3)の正規分布
}

念のためARモデルのモデル式を再掲

$y_t = c + \sum_{i=1}^{p}a_py_{t-p}+\epsilon_t$

コレログラムは以下

上側がプロット、左下が自己相関、右側が偏自己相関を示す。
(自己相関はn時点前との相関、編自己相関は1〜n-1時点までの相関による影響を排除した、n時点前との相関)
自己相関および偏自己相関のグラフは、n時点前との相関の強さを示し、青い点線よりグラフが上なら有意な自己相関がある。

編自己相関を見ると、一つ前の時点の値との相関はあるが、それ以外との相関はない事がわかる。
これはAR(1)のモデルと一致する。

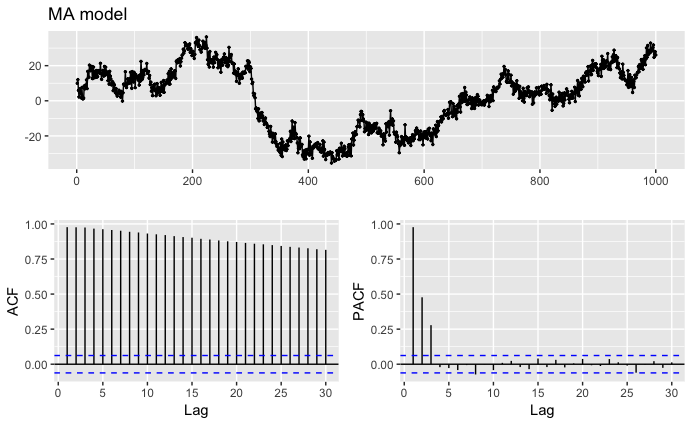
４. MAモデルのシミュレーションとコレログラム

MAモデルは、以下のようにして作成できる。

ma = 10 #初期値
q = 3 #何回分の平均とするか
#一旦thetaは1で固定
for(i in 2:q){
  ma[i] <- mean(ma[1:(i-1)]) + rnorm(1,sd=3)
}
for(i in (q+1):1000){
  ma[i] <- mean(ma[(i-q):(i-1)]) + rnorm(1,sd=3)
}

念のためMAモデルのモデル式を再掲

$y_t = \mu + \epsilon_t + \sum_{j=1}^{q}\theta_j \epsilon_{t-j}$

コレログラムは以下

同様に、編自己相関を見ると3時点前までとの相関がある事がわかる。
これはMA(3)のモデルと一致する。

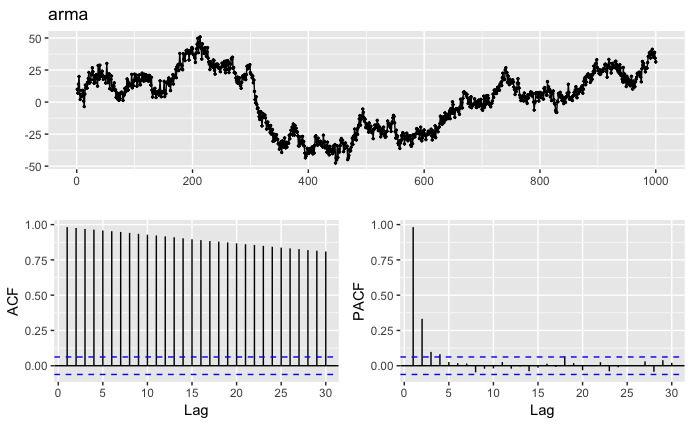
５. ARIMAモデルのシミュレーションとコレログラム

ARMAモデルは、以下のようにして作成できる。


arma = 10 #初期値
fai = 0.2
q = 3
noise = 1
#p=1, theta=1

for(i in 2:q){arma[i] <- mean(arma[1:(i-1)]) + arma[i-1] * fai + rnorm(1,sd=3) * noise}
for(i in (q+1):1000){arma[i] <- mean(ma[(i-q):(i-1)]) + arma[i-1] * fai + rnorm(1,sd=3) * noise}
ggtsdisplay(arma)

コレログラムは以下

MAモデルよりも1時点前との相関が強くなっている(2,3時点との相関が弱くなっている)事がわかる。
これは、ARモデルの１時点前の要素の影響を受けて、相対的に2,3時点前の影響が弱くなっているため。

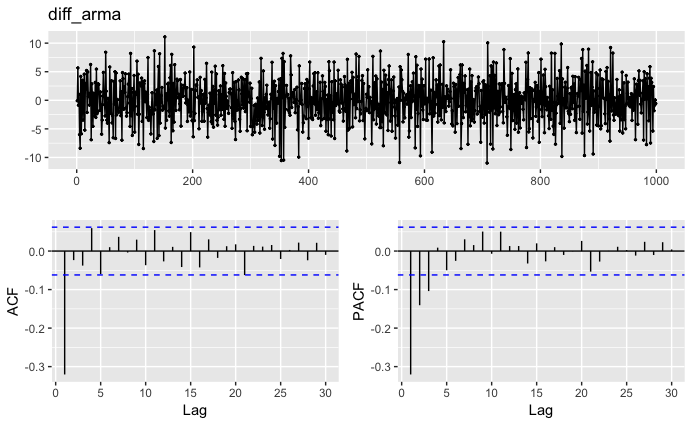
なお、定常性を持たせるには1階差分をとれば良い。


diff_arma <- diff(arma, lag=1)
ggtsdisplay(diff_arma)

コレログラムは以下となる。

6. Rのパッケージを使用したARIMAモデルの作成(arima.sim)

同様のシミュレーションはarima.simを使用して作成できる。

以下はARIMA(1,1,3)のモデル


arima_sm <- arima.sim(n=1000, #出力数
                   list(order=c(1,1,3),  #AR(p,d,q)を示す。
                        ar=0.1,#ARモデルの係数(ファイ値)
                        ma=c(1,1,1)),#MAモデルの係数(theta値)
                   sd=3) #ホワイトノイズの標準偏差
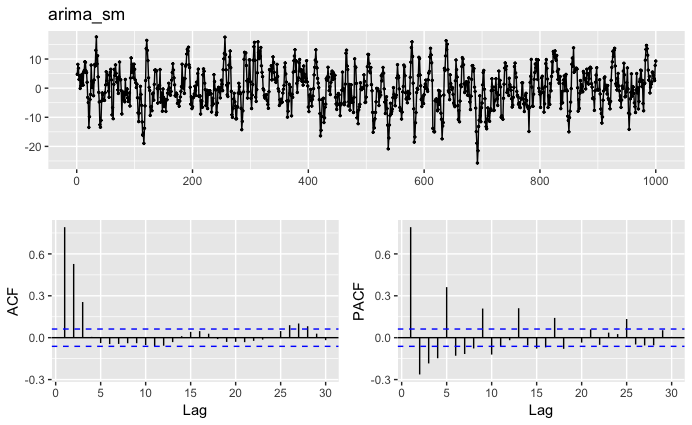
ggtsdisplay(arima_sm)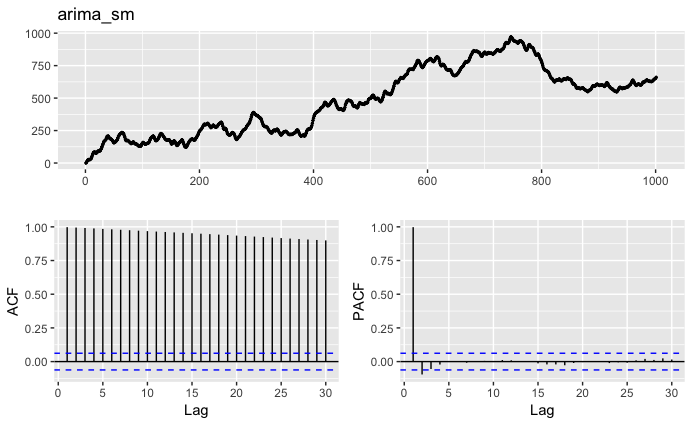

上記では、1階差差分(order[2]=1)を設定しているため、定常過程ではない。

階差差分を0とする。ARIMA(1,0,3)


arima_sm <- arima.sim(n=1000, #出力数
                   list(order=c(1,1,3),  #AR(p,d,q)を示す。
                        ar=0.1,#ARモデルの係数(ファイ値)
                        ma=c(1,1,1)),#MAモデルの係数(theta値)
                   sd=3) #ホワイトノイズの標準偏差
ggtsdisplay(arima_sm)

以下のように定常過程となっている事がわかる。