離散型の確率分布である二項分布の概要や使い方についてまとめました。
~目次~
1. ベルヌーイ試行と二項分布の概要
ベルヌーイ試行とは、成功と失敗やコインの表裏のような二つの結果をもたらす試行をn回繰り返す試行をいいます。
この試行は独立(各試行が他の試行に影響を与えない)かつ、同じ条件である必要があります。
二項分布とは、このベルヌーイ試行の確率分布のことを言い、Bi(n, p)で表します。
ここで、nは試行回数、pは成功確率を示します。
2. 二項分布の確率分布関数
二項分布の確率分布関数は以下の式で表されます。
上記の式はpがx回成功する確率(![]() )、pがn-x回失敗する確率(
)、pがn-x回失敗する確率(![]() 、成功がn回の試行のどのx回で発生するか(
、成功がn回の試行のどのx回で発生するか(![]() )の積で計算されています。
)の積で計算されています。
以下の例題を解いてみましょう。
ハートがトランプに占める割合pは4分の1(0.25)となりますので、計算は以下になります。
f(x)が確率分布関数であることの証明
f(x)が確率分布であるには、f(x)の総和が1であることを証明する必要があります。
これは二項定理の逆のそのままのため、簡単に証明できます。
![]() ・・・(1)
・・・(1)
(参考)二項定理は以下になります。
![]()
3. 二項分布の期待値と分散の導出
二項分布の期待値と分散は以下になります。
それぞれの計算方法は以下になります。
二項分布の期待値の導出
上記の確率分布関数から期待値を求めます。
![]() ・・・期待値の公式より
・・・期待値の公式より
![]()
・・・分子のxで分母のx!を払い、![]() のpとnを
のpとnを![]() の外に出します
の外に出します
![]()
・・・Cの分解式より![]()
![]()
![]()
・・・(1)式より![]()
![]()
n回コインを投げた時の成功回数の期待値はnpというのは直感とも合うかと思います。
二項分布の分散の導出
期待値と同様に求めます。
以下の公式を使います。
![]()
上式の右辺を求めます。
![]()
![]()
・・・x=0の時![]() より
より
![]()
・・・x=y+1とします
![]()
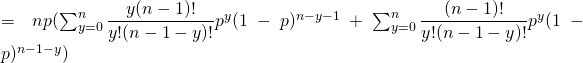
和の左側と右側を分けて計算します。
![]()
・・・分子のyでy!の次数を一つ下げ、pと(n-1)を外に出します。
![]()
![]()
![]()
続いて右側を計算します。
![]()
![]()
![]()
以上から、![]() の左項は以下になります。
の左項は以下になります。
![]()
また、![]() の右項は以下になります。
の右項は以下になります。
![]()
以上から、
![]()
![]()
![]()
4. 二項分布の導出(モーメント)
続いて、モーメント(積率母関数)を用いて期待値と分散を導出します。
モーメント関数の定義および公式は以下になります。
二項分布のモーメント母関数
二項分布のモーメント母関数を求めます。
![]()
・・・3章と同様に、![]() より
より
![]()
![]()
・・・二項定理から(詳細は2章参考)
![]()
二項分布のモーメント母関数の1回微分と期待値
1-p=qと置くと、モーメント母関数の1回微分は以下になります。
![]()
・・・![]() より
より
以上から、期待値は以下になります。
![]()
二項分布のモーメント母関数の2回微分と分散
同様に、2回微分は以下になります。
![]()
以上から、分散は以下になります。
![]()
![]()
5. 二項分布のRでの使用方法
成功回数がnとなる確率(dbinom)
二項分布をRで導出するにはdbinom関数を使用します。
使い方は以下になります。
x: 成功回数
n: 試行回数
p: 成功回数
2章の例題を解いてみます。
ハートがトランプに占める割合pは4分の1(0.25)となりますので、以下になります。
> n <- 5
> p <- 0.25
> dbinom(x,n,p)
[1] 0.2636719
成功回数がn以上(累積分布)となる確率(pbinom)
n個以上となる方法を求める場合はpbinom関数を使います。
パラメータの入れ方はdbinom関数と同じになります。
ただし、pbinom関数はn回以下となる確率なので注意しましょう。
以下の例題を解いてみます。
4枚以上の確率は、ハートが3枚以下である確率を引いて(余事象)求めます。
> n <- 7
> p <- 0.25
> 1-pbinom(x,n,p)
[1] 0.07055664
以上から、約7%となることが分かりました。
確率qで、成功回数がx回以下となるxの値(分位関数)を求める方法(qbinom)
これはpbinom関数の逆関数になります。
別の言い方をすると、成功回数が0回からx回までの累積確率がqを超えない最大のxを返します。
使い方は以下になります。
q: 成功回数がx回以下となる確率
n: 試行回数
p: 成功回数
具体例を見てみましょう。
計算してみましょう。
> n <- 3
> n <- 7
> p <- 0.25
> qbinom(q,n,p)
[1] 2
つまり、7枚トランプを引いた時に、ハートの枚数が0-2枚である確率は、50%以上であり、0-1枚である確率は50%以下ということです。
pbinom関数を使って確認してみます。
[1] 0.7564087
> pbinom(1,n,p)#ハートがが0-1枚である確率
[1] 0.4449463
以上です。
二項分布の乱数の出力(rbinom)
二項分布の乱数はrbinom関数で出力できます。
使い方は以下になります。
N: 出力する乱数の個数
n: 試行回数
p: 成功確率
例えば、7枚カードを引いた時のハートの枚数を数える試行を、15回行います。
> n <- 7
> p <- 0.25
> rbinom(N,n,p)
[1] 1 1 3 1 1 3 0 2 0 2 1 2 1 4 3
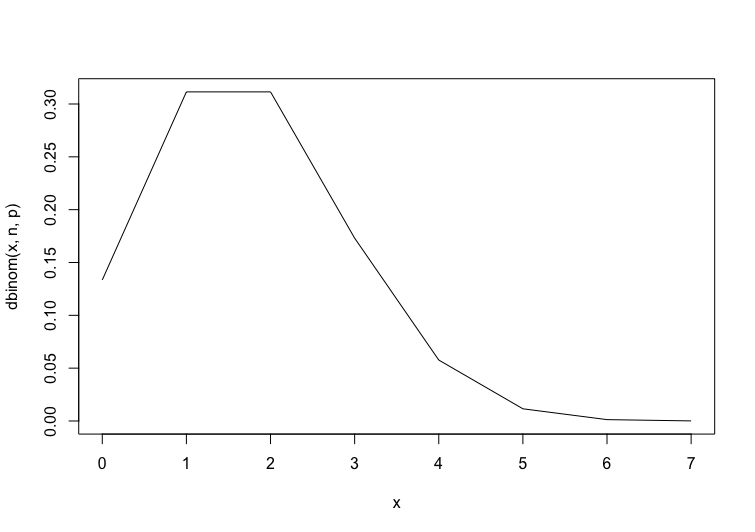
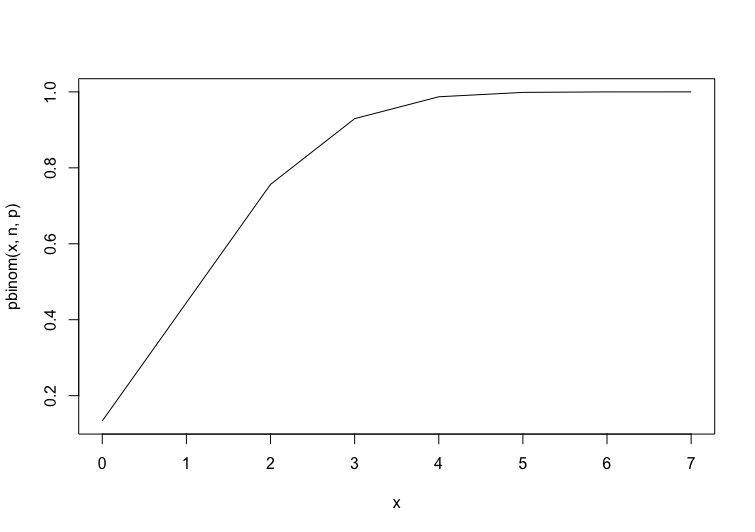
二項分布の確率分布関数と累積確率分布関数のグラフの書き方
上記で使用したdbinom関数と、pbinom関数を使用します。
トランプをn回引いた時に、ハートの枚数をx軸に、x枚である確率をy軸にプロットします(確率密度関数)。
同様に、x枚以下である確率をy軸にプロットします(累積確率密度関数)。