代表的な統計的仮説検定の相関検定について、その概要とR言語を用いた具体的な検定方法についてご紹介します。
※使用するデータはすべてプロ野球データFreak様からお借りしています。
1変数のt検定については、(t検定の方法)ををご参照ください。
~目次~
1. 相関係数の検定(無相関検定)とは
相関係数の検定(以下相関検定)とは、母集団に相関があるかどうか(有意かどうか)を、標本データから推測する検定手法です。
※相関係数とは、二つのデータの間の相関(片方が上がれば、もう片方も上がる(下がる))の強さを測る統計量です。
あくまで、相関が有意かどうかを確認するものであって、相関の強さを確認するものではありません。
ただし、直感的にわかるかと思いますが、結果として標本データの相関が強い(相関係数が大きい)ものほど、有意である可能性は高くなります。
2. 相関係数の検定の手順
相関検定の手順のベースは統計的仮説検定と同様になります。
統計的仮説検定の詳細は【R言語と統計の備忘録】統計的仮説検定もご参照ください。
なお、先ほど述べたように、相関検定は標本データ間の相関が有意かどうか、を確認するものであり、帰無仮説もそれに従います。
3章では以下の手順に沿って検定を行なっていきます。
統計的仮説検定の手順
1. ある事象について、検定したい仮説(帰無仮説)を決める
2. 仮説を検定するための検定統計量(標本統計量)を選択する
3. 検定の判断基準(有意水準)を設定する(現実的に起こりうるものかどうかの基準)
4. 今回の事象に対する検定統計量を計算(実現値)し有意水準と比較することで、仮説の正否を判断する。
3. 相関検定の具体例 ~プロ野球の盗塁と順位に相関はあるか~
この章では相関検定の方法について、具体例を用いてご説明します。
盗塁は犠打と並んで、「実は有効な戦術では無い」と言われることも多く、一般的に盗塁成功率が8割以上ないと損をする戦術と言われます。
そこで、今回はプロ野球の順位と盗塁に相関があるのかどうか、を検定します。
0. 事前準備
はじめに、データの状況を確認しておきましょう。
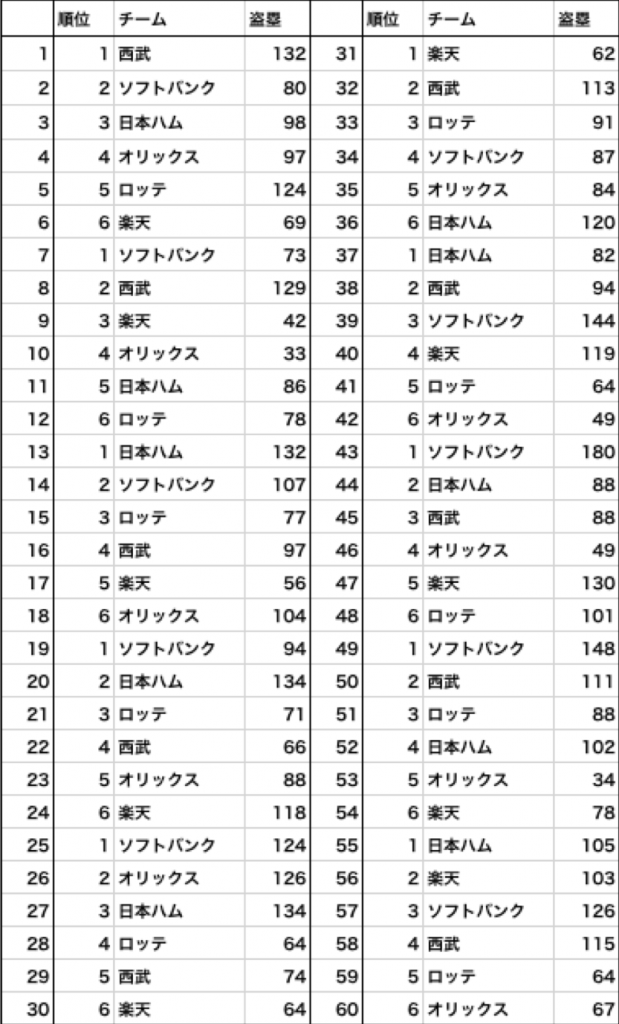
以下は、今回使用する2009年-2018年の10年間の順位と盗塁数の表になります。
数字だけ見てもピンと来ませんね。
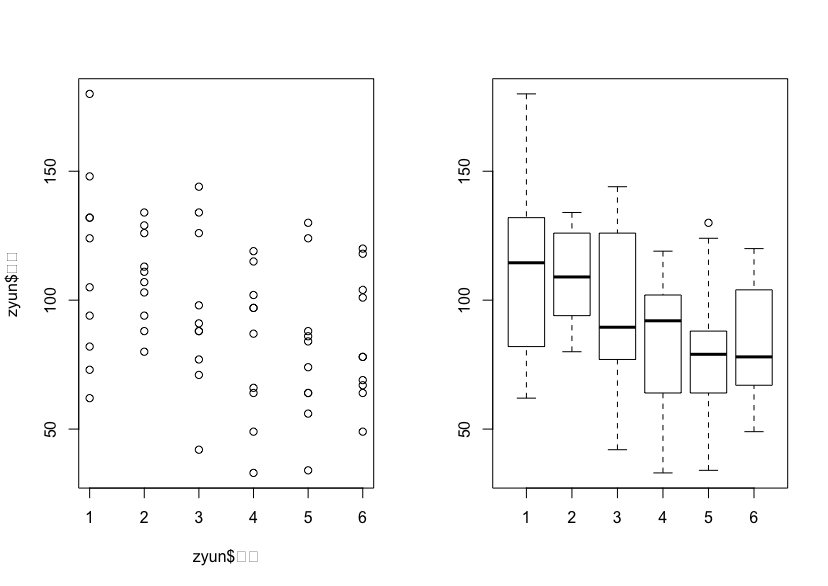
では、次にグラフで可視化して見ましょう。
以下は散布図と箱ひげ図で、横軸を順位、縦軸を盗塁数でとっています。
この図をみると、上位の方が盗塁数が多いように見えますね。ただ、そこまで大きな差はない傾向です。
 最後にこの二つのデータの相関係数を求めておきましょう。
最後にこの二つのデータの相関係数を求めておきましょう。
Rのcor関数を使います。
> cor(zyun$順位, zyun$盗塁)
[1] -0.389192
-0.4弱と、多少ですが相関はあります。ただしこの相関はあくまで標本データの相関であって、母集団(この場合は未来も含めたプロ野球のすべての年の順位と盗塁)に相関があるのかを示しているわけではありません。
母集団に相関があるかどうかは、検定を行なって確認していきます。
1. ある事象について、検定したい仮説(帰無仮説)を決める
今回の帰無仮説は、前置きで述べたように盗塁と順位の相関の有無になります。
そこで、以下のような帰無仮説を設定します。
盗塁と順位には相関関係は無い
なお、あくまで"相関関係がない"ことを帰無仮説とするため、両側検定とします。
(盗塁と順位の相関が、負の相関であっても、正の相関であっても帰無仮説を棄却します)
2. 仮説を検定するための検定統計量(標本統計量)を選択する
相関係数の検定では、以下の検定統計量を使用します。
![]()
r: 標本相関係数
n: 標本のデータ数
なお、なぜ上記の値を使用するかについては、ここでは省略します。
(実際の計算は手順4で実施します)
3. 検定の判断基準(有意水準)を設定する
今回は、両側検定で、有意水準を5%と設定します。
4. 検定統計量を計算(実現値)し有意水準と比較することで、仮説の正否を判断する。
このステップでは①実現値の計算と、②設定した有意水準における棄却域の実現値の値の確認、③導出した二つの値の比較、の順で実施します。
まず、①検定統計量の実現値を計算していきます。
まず、標本データの相関係数rは先ほど求めた通り、以下になります。
> cor(zyun$順位, zyun$盗塁)
[1] -0.389192
続いて、標本数nは以下になります。
> length(zyun$順位)
[1] 60
以上から、標本統計量を計算しましょう。
> n <- length(zyun$盗塁)
> r <- cor(zyun$順位, zyun$盗塁)
> t <- r*sqrt(n-2)/sqrt(1-r^2)
> t
[1] -3.217691
t=-3.2177と計算できました。
続いて、②有意水準5%の両側検定における棄却域(帰無仮説が棄却される検定統計量の境界値)を求めます。
これは、t分布表(参考)を参照する方法もありますが、ここではRのqt関数で導出します。
> qt(0.025,58)
[1] -2.001717
ここで、有意水準5%で両側検定のため、0.05の半分の0.025を使用しています。
また、58は自由度(df)であり、データ数(60)-2=58 を使用します。
③最後に、二つの値を比較しましょう。
今回①で求めたt値の絶対値が、②で求めた値の絶対値よりも大きいため、帰無仮説は棄却されます。
(実現値が棄却域に入る、という言い方をします)
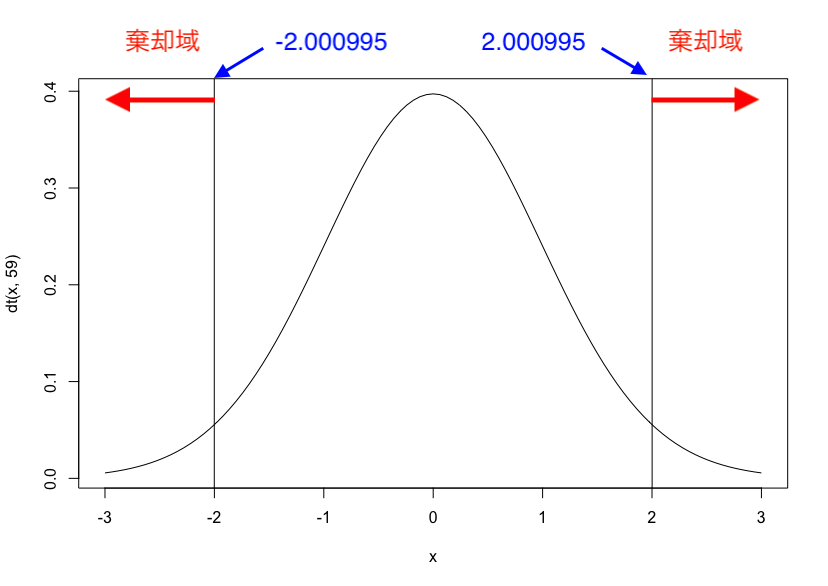
これを図示すると以下のイメージになります。
釣鐘型のグラフが、t検定で、df=59のグラフになります。
x=2と-2付近にある縦の線が上記でqtで求めた有意水準の境界です。
今回のt値の-3.2がこれの外側の棄却域にあるため、帰無仮説は棄却されます。
以上から、"盗塁と順位の間の相関は有意ではない"という帰無仮説が棄却された結果、"盗塁と順位の間の相関は有意である"という結果になります。
4. Rでの相関検定の関数(cor.test)
Rには、相関検定を簡単に行うための関数、cor.testが用意されています。
使い方は以下となります。
cor.test(<<データ1>>, <<データ2>>,[conf.level=<<有意水準>>])
※有意水準のデフォルト値は0.95(5%で有意)
実際に今回の例で計算して見ましょう。
> cor.test(zyun$盗塁, zyun$順位)
Pearson's product-moment correlation
data: zyun$盗塁 and zyun$順位
t = -3.2177, df = 58, p-value = 0.002116
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.5852765 -0.1501011
sample estimates:
cor
-0.389192
出力された値を見ると、3行目に以下の出力があります。
t = -3.2177, df = 58, p-value = 0.002116
tが先ほど求めた実現値、dfが自由度、p-valueが有意水準5%での境界値となっていることがわかります。
また、最後の列には相関係数rも出力されています。
この結果からも、t > p-valueとなっており、帰無仮説が棄却されることが簡単にわかります。
以上、相関検定の手順と、その具体例、またcor.testを使用した簡単な検定方法についてご紹介しました。