【統計学とRの備忘録】様々な相関係数の概要と公式・Rの関数

二つ(以上)のデータの関係の程度を表す方法として相関係数がありますが、相関係数には様々な種類があります。

本記事では、様々な種類の相関係数の概要について簡単にまとめました。

相関係数の検定については以下のページをご覧下さい。
【R言語と統計の備忘録】相関係数の検定の手順と具体例【プロ野球の順位と盗塁数に相関はあるか】

～目次～

1. ピアソンの積率相関係数

2. 編相関係数

3. 順位相関係数(スピアマンの順位相関係数とケンドールの順位相関係数)

4. 系列相関係数(自己相関係数)

１. ピアソンの積率相関係数

ピアソンの積率相関係数とは

ピアソンの積率相関係数(product-moment correlation coefficient)は最も一般的な相関係数であり、二つのデータの間の相関(関係)の強さを示した値です。

単に相関係数といえばこの値を指し、二つのデータ間の偏差と分散を利用したパラメトリックな方法です。

パラメトリックとノンパラメトリック

パラメトリック手法とは、対象となるデータの分布の詳細が分かっている場合に使用する。
対象とする統計量としては、平均値や分散。
尺度水準は間隔尺度と比例尺度のみを扱い、名義尺度や順序尺度は扱えない。

一方で、ノンパラメトリック手法はデータの詳細な分布がわかっていない(利用しない)場合に使用する。例えば、データの順位や分類に関する情報を使用する。
対象とする統計量としては代表値や度数、順位など。
尺度水準は名義尺度・順序尺度・間隔尺度・比例尺度の全ての水準を扱える。

ピアソンの積率相関係数の定義

定義式は以下となり、データが一つの場合の分散の式に非常に似ています。

r = $\dfrac{(x_1 - \bar{x})(y_1 - \bar{y}) + (x_2 - \bar{x})(y_2 -\bar{y}) ... (x_n - \bar{x})(y_n - \bar{y})}{n}$
・ $\bar{x}, \bar{y}$ は、それぞれx,yの平均を示す。
・nはx, yのデータ数

rの値は-1から1の間をとり、-1なら完全な負の相関、0なら相関無し、1なら完全な正の相関を示します。

Rでのピアソンの積率相関係数

Rで計算する際は、cor関数を使用します。

> a <- c(1,2,4,5,8)
> b <- c(20,23,15,30,40)
> cor(a,b)
[1] 0.7896467

詳細については、以下記事の3章にまとめていますので、そちらをご覧下さい。
【R言語と統計の備忘録】共分散と相関係数とファイ係数【多変数統計量】

２. 編相関係数

編相関係数とは

編相関係数(partial correlation coefficient)とは、二つのデータの間の相関係数を、"二つのデータ以外の第三のデータ"による影響を除外した相関係数となります。

例えば、データA, B, Cがあったときに、データAとBの間だけの純粋な相関を求めるために、Cによる影響を除外して計算された相関係数です。

更に具体的に言うと、"収入(データA)"と"病院に行く回数(データB)"の間に正の相関が見られたとします。
(これを見かけ上の相関と言います)
しかし、普通に考えて収入が多くなると病気になりやすいかというとそうではありません。
この裏には潜在的な要因として、"年齢が高い(データC)"という3つ目の共通の要素があり、それの影響で相関が高く見えた可能性があります。

この"潜在的な要因"を排除したものが編相関係数となります。

編相関係数の定義

編相関係数は、以下の式で求められます。

$r_{12-3} =\dfrac{r_{12}-r_{13}r_{23}}{\sqrt{1-r_{13}^2}\sqrt{1-r_{23}^2}}$
・$r_{12}, r_{13}, r_{23}$は、それぞれデータ1,2・1,3・2,3間のピアソンの積率相関係数を示す

なお、上記の定義からもわかる通り１章で説明したピアソンの積率相関係数の一部となっています。

Rでの編相関係数の導出

pcor関数を使用することで求めることができます。
使用する際はppcorパッケージが必要となります。

使い方は以下となります。

>ppcor(<<データフレーム>>[, method = c("pearson", "kendall", "spearman")])

データフレームには、求めたい二つのデータ及び、三つ目以降の要素も含めたデータフレームを入れます。

以下では、本塁打の影響を除外して、打率と打点の相関を求めたい場合の具体例を記述します。
aveに打率のベクトル、HR列に本塁打のベクトル、point列に打点のベクトルを入れたデータフレムtmpを作成し、それについて編相関係数を求めています。
pcorでは、一つ目・二つ目と三つ目以降のデータを区別しないため、全ての直積の潜在要因を除いた編相関係数を導出します。

$estimateの箇所に、上記の定義式に則った他の要素を排除した相関係数が出力されます。

> library("ppcor") #パッケージのインストール
> tmp <- data.frame(ave=打率, HR=本塁打, point=打点) #データフレーム 
> pcor(tmp)
$estimate
             ave         HR     point
ave    1.0000000 -0.2473817 0.4407455
HR    -0.2473817  1.0000000 0.8565684
point  0.4407455  0.8565684 1.0000000

$p.value
               ave            HR         point
ave   0.000000e+00  9.411683e-12  2.005240e-36
HR    9.411683e-12  0.000000e+00 1.164972e-213
point 2.005240e-36 1.164972e-213  0.000000e+00

$statistic
            ave        HR    point
ave    0.000000 -6.926589 13.32074
HR    -6.926589  0.000000 45.03219
point 13.320742 45.032188  0.00000

> cor(打点, 打率)
[1] 0.4576976

本塁打の要素を含んだ相関は"cor(打点, 打率)"より"0.458"、本塁打の要素を排除した値は"0.441"となっています。
この二つに違いがないことから、打率と打点の相関に本塁打は大きな影響は与えていないことがわかります。

３. 順位相関係数

順位相関係数の概要

順位相関係数とは、二つの質的基準(尺度水準でいうところの名義尺度・順序尺度)がある場合に、二つの基準による順位の相関を示す係数です。
例えば、英語の試験と数学の試験を同じ人が受けたときに、それぞれの点数は不明であるが順位のみ分かっている時に、英語の試験の順位と数学の試験の順位に相関があるかどうか確認する場合などに使用されます。

代表的なものとしてスピアマン(C. Spearman)によるスピアマンの順位相関係数と、ケンドール(M. G. Kendall)によるケンドールの順位相関係数があります。

スピアマンの順位相関係数の定義とRでの導出方法

スピアマンの順位相関係数の定義

スピアマンの順位相関係数($r_s$とする)は、基本的にはピアソンの相関係数がデータ値で計算するところを、順位で計算したものとなります。

定義式は $r_s=\dfrac{V_{xy}}{\sqrt{V_xV_y}}$ であり、通常の相関係数と同様になります。
※ $V_{x}, V_{y}$ はそれぞれx, yの分散であり、 $V_{xy}$ は $\bf{X}, \bf{Y}$ の共分散

ただし、順位相関係数では順位しか扱わないため、以下の式で計算することが可能です。

$r_s=1-\dfrac{6}{n^3-n}\sum_{i=1}^{n}(\bf{R}_i-\bf{R}_i')^2$
※ $\bf{R}_i$ は各要素の順位を、nは要素数を表す

例えば、英語と数学でAさんからEさんまで5人の人の順位相関を求めたい場合は、 $\bf{R}_1$ はAさんの英語の順位、 $\bf{R'}_1$ はAさんの数学の順位を入れます。

スピアマンの順位相関係数のRでの導出

通常の相関係数と同様にcor関数を使用します。

>cor(<<データ1>>, <<データ2>>, method="spearman")

methodオプションは、デフォルトではピアソンの積率相関係数を使用するようになっています。
methodで指定できるのは"pearson" "kendall" "spearman"の3つになります。
データ1とデータ2は順位のデータでなくても、自動的に順位のデータにて計算してくれます。

具体例を見て見ましょう。

> cor(打点, 打率, method="spearman")
[1] 0.4906152
> cor(打点, 打率)
[1] 0.4576976

以下のようにピアソンの積率相関係数とは異なった値が出ているのがわかるかと思います。
大小関係については特になく、データによります。

ケンドールの順位相関係数の定義とRでの導出方法

ケンドールの順位相関係数の定義

ケンドールの順位相関係数( $r_k$ )は、二つのデータについて同じ二つの要素のペアを抽出し、それの順位の大小を見ます
そして、二つのデータについて、選んだペアの順位の大小が同じなら+1, 異なる場合は-1をしてそれらを足していき、最後にペアの数で割り平均を出します。
他の相関係数と同様に、-1から1の範囲で値をとります。

もう少し具体的に見ていきましょう。
二つのデータの順位が入ったベクトルを $\bf{X}, \bf{Y}$ とし、観測対象のペアをi番目とj番目とします。(i,j=1, 2, 3 ..., n)
( $\bf{X}_i, \bf{X}_j$ )と( $\bf{Y}_i, \bf{Y}_j$ )の順位の大小が同じ(両方ともiが大きい/小さい)場合は1を、異なる場合は-1を足していきます。
これは、数学と英語の点数の大小がAさんとBさんで同じ(二人とも数学(英語)の方が点数が高い)場合は１を足すことを意味します。

式で表すと以下になります。

$r_k=\dfrac{G-H}{n(n-1)/2}$

ここで、Gは順位の大小が同じ(+1をする)ペアの数、Hは順位の大小が異なる(-1をする)ペアの数を示します。

ケンドールの順位相関係数のRでの導出方法

通常の相関係数と同様にcor関数を使用します。

>cor(<<データ1>>, <<データ2>>, method="kendall")

具体例は以下になります。

> cor(打点, 打率, method="kendall")
[1] 0.3442683

スピアマンの順位相関係数とケンドールの順位相関係数の違い

二つの値自体に優劣はないため、どちらを使うかについては検定者の考えによるところとなります。
ただし、一つの相関係数を選んだ場合は同じ係数を使用しましょう。

二つの順位相関係数について、主に以下の特徴があります。

この二つの相関係数自体は、計算方法も全く異なるため、相関係数も異なった値を示す。
二つとも"検定力"と呼ばれる正しく帰無仮説を棄却する確率は同じ。
スピアマンの相関係数の方が大きい値を示すことが多い(目安として1.5倍程度)

４. 系列相関係数(自己相関係数)

系列相関係数(自己相関係数)の概要

上記で説明した相関係数は、二つの異なる人や環境間の関係の大きさを示すものでした。

一方で、系列相関係数(serial correlation coefficient)とは(自己相関係数(auto-correlation coefficient)、以下：系列相関係数)、同じ対象の過去のデータと現在のデータとの相関の大きさを示します。
これは、過去のデータとの因果関係や、データの周期などを調べるために使用します。

例えば、毎月集計している店舗の売り上げを、１ヶ月前との相関を調べることで、来月の需要の予測に使用したりします。
今、 $\bf{X}=x_0, x_1, ... x_n$ というnヶ月の売り上げのデータがあるときに、比較対象のデータとして $\bf{Y}=x_1, x_2...x_{n+1}$ を使用して、 $\bf{X}$ と $\bf{Y}$ の間の相関を求めます。

系列相関係数(自己相関係数)の定義

系列相関係数の定義は、以下になります。

$r_h=\dfrac{\sum_{i=1}^{n-h}(x_i-\bar{x})(x_{i+h}-\bar{x})/(n-h)}{\sum_{i=1}{n}(x_i-\bar{x})^2/n}$
h: 遅れの値(３カ月前との比較をする場合はh=3)
$\bar{x}$ : $\bf{X}$ の平均値

なお、普通に考えるとhが大きくなると時間の間隔も大きくなるため、相関係数の値も0へ近づくことが予想されるが、例えば季節や年の変動等がある場合には、特定の値で強い相関が出る場合がある。
(毎年12月には売り上げが高い等)

この式を見ると、分子の $(x_i-\bar{x})(x_{i+h}-\bar{x})$ の部分から、i番目とi-h番目のデータが平均値に対して同じ向きなら $r_h$ の絶対値が増えて行くことがわかる。
例えば、常にi番目とi-h番目のデータが平均値に比べて大きいor小さいなら正の相関となり、常に片方は平均より大きく、片方は平均より小さい場合は負の相関となる。

系列相関係数(自己相関係数)のRでの導出

Rでは自己相関係数を求める関数が見つからなかったので、以下にサンプルコードを記載します。

auto_correlation <- function(x, h=1){
  n <- length(x)
  molecule <- 0 #分子
  denominator <- 0 #分母
  ave.x <- mean(x)
  for (i in 1:(n-h)){
    molecule <- molecule + (x[i] - ave.x) * (x[i+h] - ave.x) / (n-h)
  }
  for (i in 1:n){
    denominator <- denominator + (x[i] - ave.x)^2/n
  }
  r_h <- molecule/denominator
  return(r_h)
}

いくつか相関係数を導出します。

> x <- c(1,3,1,3,1,3,1,3,1,3,1,3)
> auto_correlation(x,h=1)
[1] -1
> auto_correlation(x,h=2)
[1] 1

これは、先ほど説明した通り平均値から常に等距離に異なっている(h=1)場合は負の相関に、同じ(h=2)場合は正の相関になっていることがわかります。

> x <- round(runif(10,0,5),3)
> x
[1] 2.991 1.089 0.720 4.084 1.790 2.204 0.569 4.158 4.618 1.486
> auto_correlation(x,1)
[1] -0.1802295

適当な乱数を作成して確認すると、相関が弱いことが分かります。

> x <- sin(c(1:100)/5)
> auto_correlation(x,5)
[1] 0.5470589
> auto_correlation(x,16)
[1] -0.9969295
> auto_correlation(x,8)
[1] -0.02049583

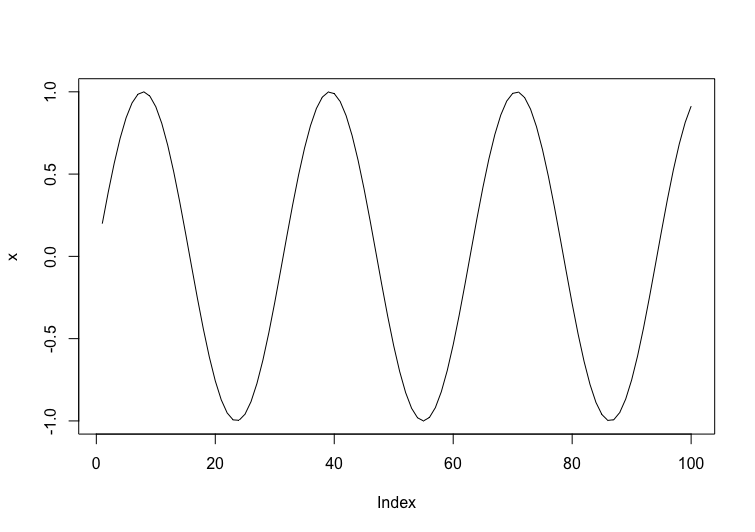
周期性のあるsinカーブでは、hの値によって周期を見つけ出すこともできます。
参考に上記のxのプロットを記載します。
x=0とx=16あたりで半周期であり、ちょうど+-が入れ替わってるのがわかるかと思います。

> plot(x, type="l")

以上です。