なっとく!アルゴリズムという本でダイクストラ法の章があったのでpythonスクラッチで書いてみました。
ソースコードだけ欲しいという方は、以下のgitを参考ください。 https://github.com/T-A0K1/Dijkstra/blob/master/djikstra_def.py
~目次~
1. ダイクストラ法とは
ダイクストラ法は、グラフ理論における最短経路探索アルゴリズムの一つです。重み付きグラフにおいいて、目的地への最短経路とそのコストを求めることができます。
制約条件として、①重みに負の値を持つことができない②閉路を持たない、という二つの条件を満たす必要があります。ただし、この制約を満たす場合においては、処理速度が速いアルゴリズムとなっています。
類似の手法として、(1)幅優先探索(重みなしのグラフにおける最短経路を求める)や、(2)ベルマンフォード法(負の値を許す)、(3)ワーシャルフロイド法などがあります。
2. ダイクストラ法の例題
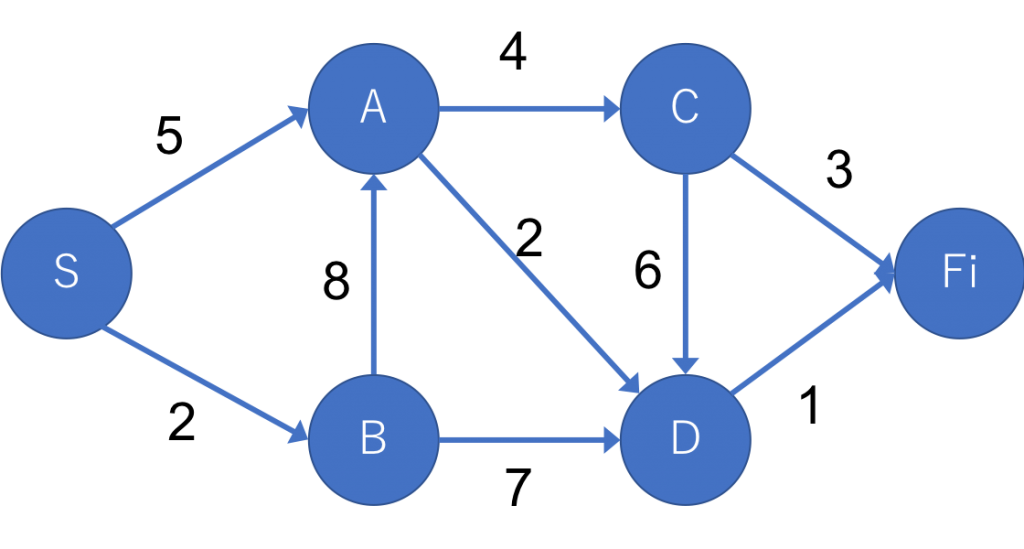
2例えば以下のようなグラフにおいて、SからFiまで行くときの最短経路を求めます。
答えはS→A→D→Fiでコストは8となります。
1章で述べたように、上記は重みに負の値がなく、また閉路(ループ経路)がないことを満たしています。
3. pythonでのコードの解説
構造について、簡単に解説します。全文は下もしくは上に記載したgitをご覧ください。
def Dijks(graph_):
processed_ = [] #処理済みノードを格納
parents_ = {} #そのノードへの直前のノードを格納
costs_ = {} #各ノードへのコストを格納
メインで使用するのは4つの辞書/リストです。 graph_は二重リストで、1段目には各ノードをキーに持ちます。2段目には各キーから繋がっているノードをキーとし、値にはそのルートへの重みが入ります。2章の例題で、一部のみ記載すると以下になります。
graph = {}
S,A,B,C,D,Fin = {},{},{},{},{}, {}
S['A'] = 5
S['B'] = 2
graph['S'] = S
processed_は処理済みのノード、parents_は現時点でのそのノードへの最短経路をたどるための1つ前のノード(例えばAの場合はSから行くのでSが入ります)。costs_は当該のノードへの現時点での最低のコストです。
"現時点"と書いたように、逐次更新されていきます。
for keys in graph_.keys():
parents_[keys] = ''
costs_[keys] = 99999 #各ノードのコストを初期化
#スタート地点を処理
for i in graph_['S'].keys():
costs_[i] = graph_['S'][i]
parents_[i] = 'S'
paretns_とcosts_を初期化します。 parents_は全て空で、costs_は無限大の値を入れます。 どこのノードの探索も行なっていない時点では、どのノードへも行けないことを意味します。
while len(processed_)<len(graph_.keys()):
#costsの中で最もコストの低いノードをリストで取り出す
tmp_node = get_min_node(costs_, processed_)
全ノードが処理済みになるまでループを繰り返します。 その際に、costs_リストにあり、最もコストの低いノードから順番に処理をするため、get_min_node()で取り出します。
#今回の経路のコストが、以前に求めた経路よりも小さければ更新する
if costs_[key] > costs_[node]+graph_[node][key]:
costs_[key] = costs_[node]+graph_[node][key]
parents_[key] = node
選んだノードから次のノードへ行くときのコストが、これまでのものより小さければそちらの方がコストが低いルートとなるため、costs_とparents_を更新します。
4. pythonでのサンプルコード
最後に、全コードと2章での例題を解くサンプルを示します。
# 辞書の値からキーをリストで返す
def get_keys_from_value(d_, val_):
return [k for k, v in d_.items() if v == val_]
#costs_辞書の中で、最も値の低いkeyを返す。ただし, processed_リストにあるキーは除く
def get_min_node(costs_, processed_):
keys_list_ = list(costs_.keys())
for i in processed_:
keys_list_.remove(i)
now_cost_ = costs_[keys_list_[0]]
for keys_ in keys_list_[1:]:
now_cost_ = min([now_cost_, costs_[keys_]])
return get_keys_from_value(costs_, now_cost_)
#ダイクストラ法
#graph_は二重辞書。1段目は全ノードをkeyに持つ。
#二つ目は1段目のノードがから接続されているノードへのキーとコストを持つ
def Dijks(graph_):
processed_ = [] #処理済みノードを格納
parents_ = {} #そのノードへの直前のノードを格納
costs_ = {} #各ノードへのコストを格納
for keys in graph_.keys():
parents_[keys] = ''
costs_[keys] = 99999 #各ノードのコストを初期化
#スタート地点を処理
for i in graph_['S'].keys():
costs_[i] = graph_['S'][i]
parents_[i] = 'S'
while len(processed_)<len(graph_.keys()):
#costsの中で最もコストの低いノードをリストで取り出す
tmp_node = get_min_node(costs_, processed_)
for node in tmp_node:
#選んだノードからいけるノードを処理する
for key in graph_[node].keys():
#今回の経路のコストが、以前に求めた経路よりも小さければ更新する
if costs_[key] > costs_[node]+graph_[node][key]:
costs_[key] = costs_[node]+graph_[node][key]
parents_[key] = node
processed_.append(node)
return costs_, parents_
def shortest_root(parents_, target_='Fin'):
root_ = [target_]
now_ = target_
while now_ != 'S':
root_.append(parents_[now_])
now_ = parents_[now_]
return root_[::-1]
例題を解くサンプルです。
graph = {}
S,A,B,C,D,Fin = {},{},{},{},{}, {}
S['A'] = 5
S['B'] = 2
A['C'] = 4
A['D'] = 2
B['A'] = 8
B['D'] = 7
C['Fin'] = 3
C['D'] = 6
D['Fin'] = 1
graph['S'] = S
graph['A'] = A
graph['B'] = B
graph['C'] = C
graph['D'] = D
graph['Fin'] = Fin
from djikstra_def import *
print('どの点への最短ルートとコストを求めますか。以下から選んでください')
print(graph.keys())
target = input()
costs, parents = Dijks(graph)
print('ゴールへの最短コスト:', costs[target])
print('最短経路のリスト:', shortest_root(parents, target))