離散型の確率分布である超幾何分布の概要や使い方についてまとめました。
~目次~
1. 超幾何分布の概要
超幾何分布は、AがM個とBがN-M個の二つからなるN個の中からn個取り出した時に、Aがx個含まれる確率の分布です。
使用する目的として以下のような例があります。
- リンゴをa個と梨をb個混ぜたものから、無作為にn個とった時に、リンゴがx個以上含まれる確率
- ある湖に、印のついた魚をn匹放流する。数日後に、魚をM匹捕まえたところ、10%が印のついた魚だった。
そこから、湖全体に魚がどれぐらいいるかを推定する(捕獲再捕獲法) - 1000本のくじに10本当たりがある場合に、100本引いた時に当たりがn本の確率
なお、超幾何分布は非復元(without replacement)の場合に使用されます。
非復元とは、取り出したものを元に戻さないことを言います。
(逆に1個とっては1個もどすをn回繰り返す場合は、復元と言います。)
復元の場合は、二項分布となります。
2. 超幾何分布の確率分布関数
確率密度関数は以下になります。
N: 総数
M: 目的の物の個数
n: 取り出す個数
x: n個の中に含まれる目的の物の個数
上記のりんごと梨の例でいうと、Nがりんごと梨の合計の個数、Mがりんごの個数、nが無作為に取り出す個数、xがn個の中に含まれるりんごの個数になります。
上記式の意味としては、N個からx個取り出す全ての場合の数を計算し、n個の中にx個Mが含まれる総数を割って確率を求めています。
実際に計算してみましょう。
N=10, M=7, n=4, x=3を代入すると以下になります。
![]()
半分の確率でりんごが3個含まれていることがわかりました。
3. 超幾何分布の期待値と分散
超幾何分布の期待値と分散は以下になります。
なお、ここで![]() とすると、上記式は以下になる。
とすると、上記式は以下になる。
期待値については、取り出した数にNの割合をかけているので直感通りかと思います。
4. 超幾何分布のRでの導出とグラフの作成
n個丁度の確率を求める方法(dhyper)
超幾何分布をRで導出するには、dhyper関数を使用します。
使い方は以下になります。
x: n個の中に含まれる目的の物の個数
N: 総数
M: 目的の物の個数
n: 取り出す個数
N(総数)ではなく、N-M(目的のもの以外の個数)を使用することに注意しましょう。
2章の例(りんご7個、梨3個から、無作為に4個取り出した時にりんごが3個含まれる確率)を求めると以下になります。
[1] 0.5
n個以上となる確率(累積分布)を求める方法(phyper)
n個以上となる方法を求める場合はphyper関数を使用します。
入れる変数はdhyperと同じです。
なお、phyperはデフォルトではn個以下となる確率となりますので、注意してください。
以下の例題を解いてみましょう。
phyperは"以下"を求める確率なので、1から2個以下となる確率を引きます。
[1] 0.6666667
3個以上となる確率 = 3個か4個となる確率 のため、dhyperを使って検算してみましょう。
[1] 0.6666667
3個以上の確率となっていることを確認できました。
確率がq以上となるxの値(分位関数)を求める方法(qhyper)
x個以上となる確率がqを超えるxの値を返します。phyperの逆パターンです。
q: 目的のものがn個中x個以上となる確率
N: 総数
M: 目的の物の個数
n: 取り出す個数
例えば、n個取り出した時にqの確率で目的にものがx個以上取れると考えましょう。
ただし、あくまで超幾何分布は離散型の確率分布なため、戻り値は整数となります。
例題です。
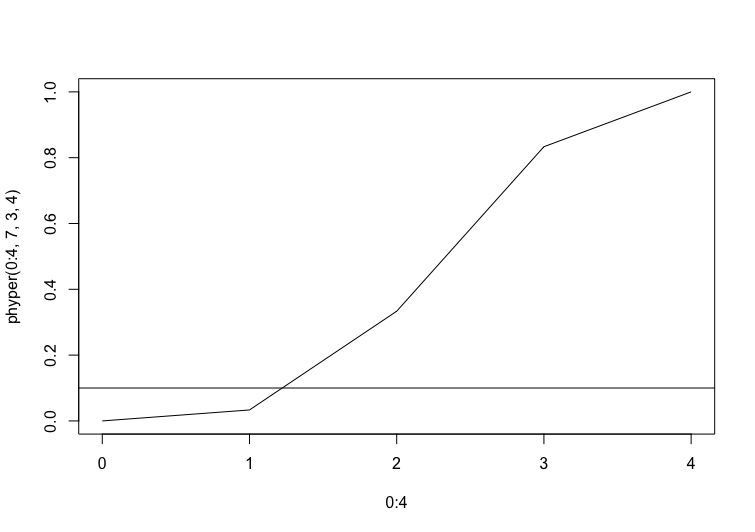
当たりを10%以下にするにはxをいくつにすれば良いか。
当たりが10%以上となるxの個数を求めます。
[1] 2
上記は、4個取り出した時に、2個以上含まれる確率が5%以上ある、ということを意味します。
そのため、"10%以下"となるxの個数は1となります。
以下が今回のりんご/梨問題の確率密度関数のプロットした結果は以下になります。横軸がxの値です。
y=0.1の線が、x=1と2の間で交わっていることが分かるかと思います。
また、グラフからhyper(0.5, 7,3,4)の結果は3になることがわかるかと思います。
5. 超幾何分布のRでのグラフの書き方
plot関数を用いると簡単です。
xにあたりの数、y軸に確率が入ります。
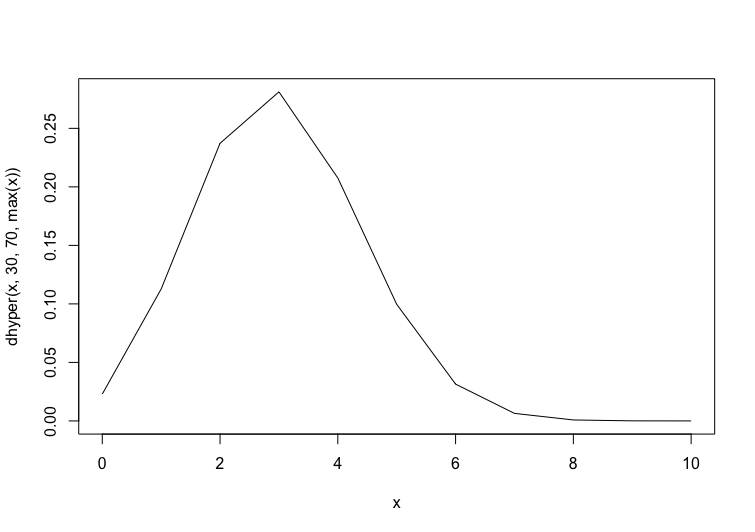
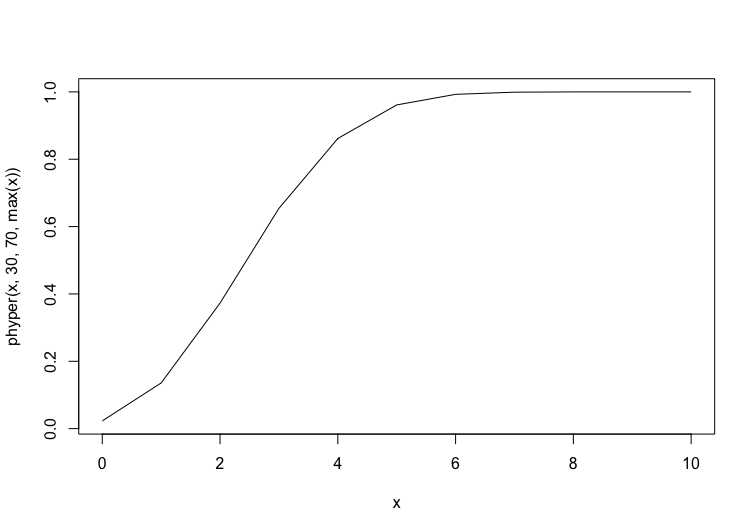
以下は、30個の当たりを含む100個の中から、10個取り出したときに当たりが0-10個となる確率分布関数および、0-10個以上となる確率密度関数になります。