基本的な統計的仮説検定の方法と、R言語を用いた具体例についてご紹介します。
統計的仮説検定とは、一言で言うと ある仮説の正否について統計的に確認する方法となります。
これだけではピンとこないかと思いますので、以下で順序を追って解説します。
本記事で使用するデータは、batter_YY にYY年の打者成績が入っています。
※使用するデータはすべてプロ野球データFreak様からお借りしています。
また、本記事の2章は"Rによるやさしい統計学(著:山田 他)"を参考にしています。
~目次~
1. 統計的仮説検定とは
統計的仮説検定とは、ある統計的事象(サイコロの出目や、ある集団のテストの平均点など)について、ある仮説を立てます。
そして、その仮説が統計的に考えて現実的に起こりうるものかどうかについて検定(判断)します。
仮説の例としては、以下のようなものが挙げられます。
- サイコロを5回振ると5回中3回6がでたが、このサイコロはイカサマのないサイコロである。
- ある集団Aとある集団Bでは平均点が10点違う。この平均点差は誤差の範囲内で、集団AとBについては学力に差がない」などです。
はじめに立てる仮説を帰無仮説と言い、通常帰無仮説は否定したいものを設定します。
2. 統計的仮説検定の手順
具体的な手順と方法についてご説明します。
手順としては、以下の4つのステップを踏みます。
1. ある事象について、検定したい仮説(帰無仮説)を決める
2. 仮説を検定するための検定統計量を選択する
3. 検定の判断基準(有意水準)を設定する(現実的に起こりうるものかどうかの基準)
4. 今回の事象に対する検定統計量を計算(実現値)し有意水準と比較することで、仮説の正否を判断する。
各ステップや語句の意味について具体例とともに順番に説明します。
0. 事象
以下の事象について、統計的仮説検定を用いて検定して行きます。
ある人がサイコロを振ると出目が5回中3回6であった。
これがイカサマなのかどうか知りたい。
1. 帰無仮説と対立仮説の設定
帰無仮説は、ある事象が特異では無いと設定し、それを否定する(その事象が特異で無いことは現実的に考えておかしい)ことで、その事象が特異であると判断します。
そこで、今回は以下を帰無仮説として設定し、それが否定できるかどうかについて検証します。
なお、帰無仮説の逆のことを対立仮説と言い、通常は証明したい内容が設定されます。
また、帰無仮説を設定すると自然と対立仮説も決まります。
今回の場合は以下となります。
2. 検定統計量の設定
次に検定に使用する標本統計量を決めます。
この、統計的仮説検定に用いられる標本統計量のことは検定統計量といい、対立仮説に合っているほど大きくなる値を設定します。
今回は以下のように設定できます。
5回サイコロを振った時に3回以上6が出る回数(確率)
標本統計量とは
例えば、有名な平均・分散・中央値・偏差値・最大(小)値・確率等は全て標本統計量になります。
ちなみに、標本とは、母集団から抽出されたデータのことを言います。
例えば、国勢調査は"標本"であり、この場合"母集団"は日本人全体をさします。
3. 有意水準の決定と棄却域・採択域について
有意水準とは、帰無仮説を採択するかどうかを判断する基準となる確率のことです。
手順2で設定した検定統計量が、今回の事象の値になる確率が、その確率と比べて高いか低いかを判断します。
つまり、現実的には起こりえない、というときの"現実的"の範囲についてとなります。
"現実的"の範囲は、一般的に5%若しくは1%と設定されます。
この5%や1%の値に学術的な意味はありませんが、慣習的にこの値が使用されています。
今回は5%と設定しましょう。
なお、有意水準の範囲のことを採択域と言い、有意水準外(現実的では無い範囲)のことを棄却域と言います。
片側検定と両側検定
この棄却域には両側検定と片側検定の2種類があります。これの違いを正規分布のグラフをもとにご説明します。
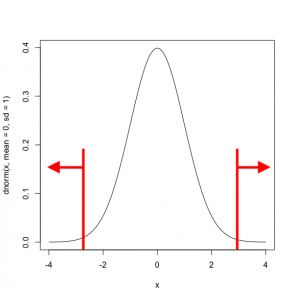
両側検定は、下記のように棄却域が両側にある検定です。
これは、例えば先ほどのコインの例だと、表と裏の両方について仮説を設定している場合、例えば"全て表もしくは裏になる"は両側検定となります。
※外側(矢印側)の領域が、帰無仮説が棄却される領域です。
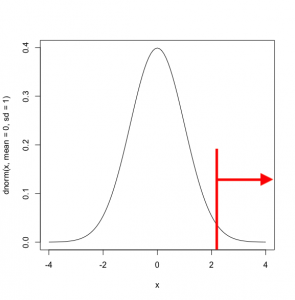
一方で、片側検定は下記のように棄却域が片側にだけある検定です。
コインの例では、コインを振った時に表もしくは裏が出る確率"どちらかだけ"について仮説を設定している場合は片側検定になります。
なお、基本的に片側検定の方が有意になる可能性が高いです。
上記のグラフを見ると、片側検定の方が両側検定よりもラインが左に寄っているのが分かるかと思います。
これは、例えば有意水準が5%の場合、両側検定では上下2.5%となるのに対して、片側検定は片方のみで5%まで有意に取ることができるためです。
4. 実現値の計算と仮説の成否
最後に、実現値の計算方法と仮説の成否の検討を行います。
実現値とは、特定の標本データから求められる検定統計量の実際の値のことを言います。
今回の場合は、"5回サイコロを振った時に3回以上6が出る回数(確率)"になります。
計算の方法としては色々有りますが、下記では3 or 4 or 5回6が出る場合の数を、全ての場合の数で割っています。
![]()
![]()
今回の実現値である0.035が、同じく今回設定した有意水準である5%(0.05)を下回っていることから、帰無仮説は棄却されます。
つまり、5回中3回6が出たこのサイコロは、何かおかしい、という対立仮説が採択されます。
以上が統計的仮説検定の流れです。
3. 統計的仮説検定の種類
今回説明した統計的仮説検定の流れは基本的な流れです。
検定手法自体は数多く有りますが、どれも今回ご説明した流れがベースとなっています。
最後に、有名な検定のいくつかを軽くご紹介します。
一つのデータに関する標本かつ、母集団が正規分布の場合の検定
標準正規分布を用いた検定
母分散が既知の場合に、標本統計量(標本平均)が母集団と同等かどうかの検定
t検定
母分散が不明な場合に、標本統計量(標本平均)が母集団と同等かどうかの検定
二つのデータの相関に関する検定
相関係数の検定
二つの標本データの母集団間の相関の有無に関する検定
二つの質的変数に関する検定
※質的変数とは、数値データではなく、男女/血液型などの分類データのこと
カイ二乗( )検定(適合度の検定)
)検定(適合度の検定)
標本データ(観測度数)の分布が、想定される母集団の分布(期待度数)と等しいかどうかを検定
カイ二乗( )検定(独立性の検定)
)検定(独立性の検定)
二つの質的変数が互いに独立であるかどうかの検定
例:血液型がO型の人の方がA型の人より和食が好きな傾向にあるかどうか
その他
独立な2群のt検定
二つの独立した標本データについて、それぞれの母集団のある統計量(平均値等)が等しいかどうかの検定
分散分析
3つ以上の標本データ間の関係に関する検定
etc..
これ以外にも、統計的仮説検定がベースとなっている検定が多くあります。
この記事が理解のきっかけになっていただければと思います。