【R言語と統計の備忘録】正規分布について【概要・グラフの描き方・乱数の出力】

正規分布概要及び見方、使い方についてRを使用しながらご紹介します。

※以下で使用するデータはすべてプロ野球データFreak様からお借りしています。
プロ野球データFreak

～目次～

1. 正規分布とは

2.【R】正規分布の描画方法

3.【R】正規分布の乱数

4.【正規分布の具体例】プロ野球選手の打率とHRは正規分布になるのか

１. 正規分布とは

概要

はじめに、正規分布(normal distribution)の一般的な定義についてご説明します。

正規分布はテストの点数や身長・体重など、非常によく見られる分布のことを言います。
そのため、母集団の分布として、とりあえず正規分布に沿った分布をしていると仮定することが多くあります。

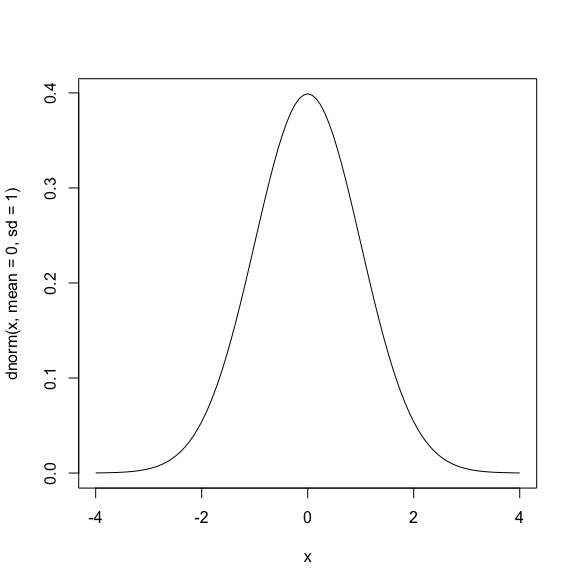
正規分布の例として、以下のようなグラフになります。

見方

正規分布のグラフは、”確率密度”を表したグラフになります。(確率密度の詳細な説明は省略します)
縦軸が当該の値になる確率です。
例えば、0になる確率が一番高く、値が上下に行くに従って確率(y軸の値)が小さくなるのが分かります。
この真ん中の0がこの分布の平均値で、平均値をとる確率が一番大きいことが分かります。

上記のグラフの分布に沿った集団においては、値がn以下(以上)になる確率は、以下になります。

n以下になる確率 = 「x<n の範囲の面積」 ÷ 「グラフ全体の面積」

正規分布の定義

正規分布自体は平均と分散の二つの統計量がわかればどのような分布になるのかが決まります。
そのため、正規分布は平均をμ、標準偏差をσとすると、以下の式でよく表されます。

N(μ, σ^2)

平均は、グラフの頂点が来る場所、分散はグラフの横幅を表します。

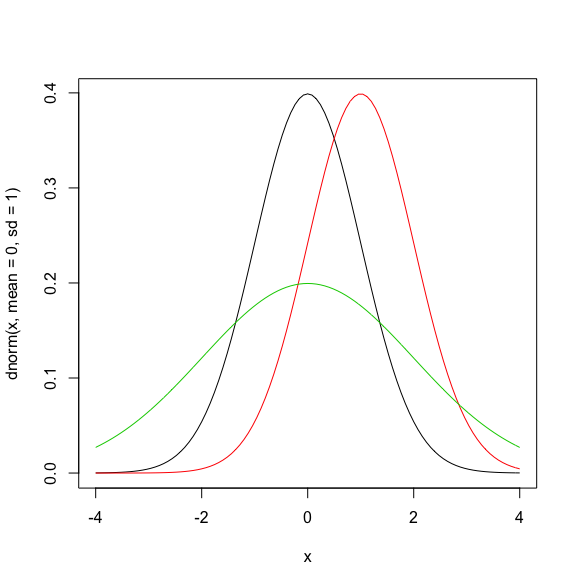
上記のグラフは、平均=0, 標準偏差=1のグラフとなりますが、平均=1, 標準偏差=1のグラフを赤で、平均=0, 標準偏差=2のグラフを緑で追記した図が以下になります。
平均が上がると右にずれ、標準偏差が大きくなると横幅が広がるのが分かるかと思います。

なお、平均はグラフの山の部分のxの値を示していることは上記で述べましたが、標準偏差もグラフ上に現れています。
標準偏差は、グラフの変曲点の位置を表しています。
変曲点とは、グラフの曲がる方向が変わる位置のことで、値の増加率のプラスマイナスが変化する点となります。

２. Rによる正規分布の描画方法

先に述べたように、正規分布は平均と分散(標準偏差)で表現されます。
そのため、図示方法は二つの統計量を使って以下で描画できます。

curve(dorm(x, mean=[平均値], sd=[標準偏差]), from=[x_1], to=[x_2])

curveはxについてのグラフを記述する関数です。
fromとtoは、表示するx軸の範囲を示します。

なお、sdとmeanは省略でき、デフォルト値はsd=1, mean=0です。

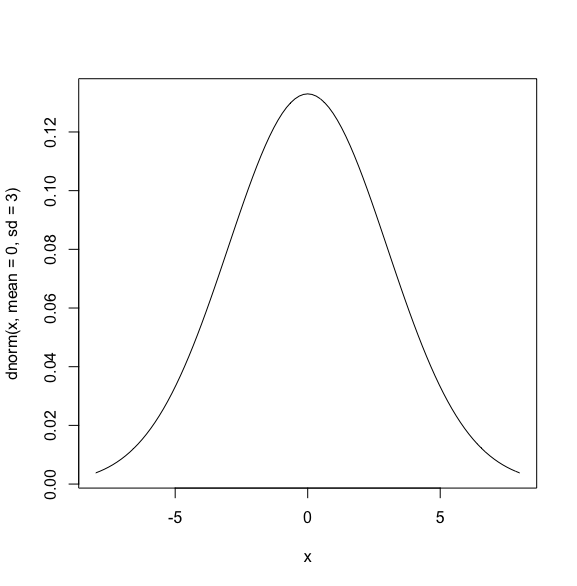
以下に例を示します。

> curve(dnorm(x,mean=0, sd=3), from=-8, to =8)
---

このように、-8から8の範囲で、平均0のグラフを描くことができました。

その他のオプション

curveには他に以下のオプションがあります
col=[数字] →線の色を指定(0:黒(デフォルト), 1:赤, 2:緑 ...)
add=[TRUE|FALSE] →今表示されているグラフに、追加で描く場合はTRUEを指定、新規で描画する場合はFALSE(デフォルトはFALSE)

３.【R】正規分布の乱数

先に述べたように、正規分布は平均と分散(標準偏差)で表現されます。
乱数についても、二つの統計量を使って以下で出力できます。

rnorm([出力数], mean=[平均], sd=[標準偏差])

なお、sdとmeanはdnormと同様に省略でき、デフォルト値はsd=1, mean=0です。

具体例は以下になります。

> rnorm(3)
[1] 0.3770742 -1.6041784 0.0972962
> rnorm(5, mean=10, sd=5)
[1] 6.781591 10.266482 10.190664 7.777987 10.104325

なお、"mean="及び"sd="の式は省略できます。
以下の二つは、同じ意味となります。

rnorm(5, mean=10, sd=5)
rnorm(5, 10, 5)

４. 【正規分布の具体例】プロ野球選手の打率とHRは正規分布になるのか

最後に、実際のデータを用いて正規分布を見ていきます。
今回は、2009年から2018年までの、規定打席1/3以上の打者の打率とHRのデータを使用します。

はじめに、打率を見てみましょう。
以下のbatter_aveには、打率が入っています。

> length(batter_ave);head(batter_ave)
[1] 739
[1] 0.327 0.317 0.314 0.314 0.312 0.309

まずデータの全容を確認するためにヒストグラムを書いていきます。

> hist(batter_ave, freq = FALSE, breaks = seq(0.15,0.425, 0.0125))
※ここでfreq=FALSEとしているのは、あとで正規分布のグラフを重ねるため"確率密度"で描画するためとなります。
---

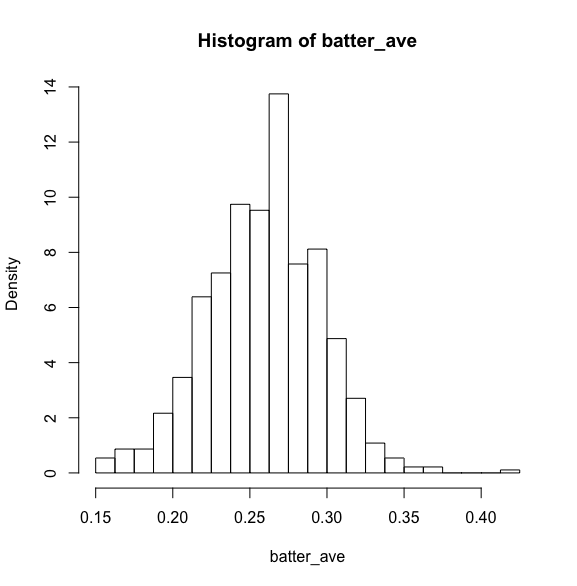
中心部が盛り上がり裾野が広がっているため、正規分布に近い形ではないかと考えられます。
※右端にある打率4割を超えているのは、2017年の日ハムの近藤選手です。

これが正規分布と同様の分布かどうかを実際に正規分布を図示して確認して見ましょう。
まずは、この打率データの統計量を確認しましょう。

> mean(batter_ave)
[1] 0.259203
> sd(batter_ave)
[1] 0.03661155

このように、平均が0.26, 標準偏差が0.0366と分かりました。
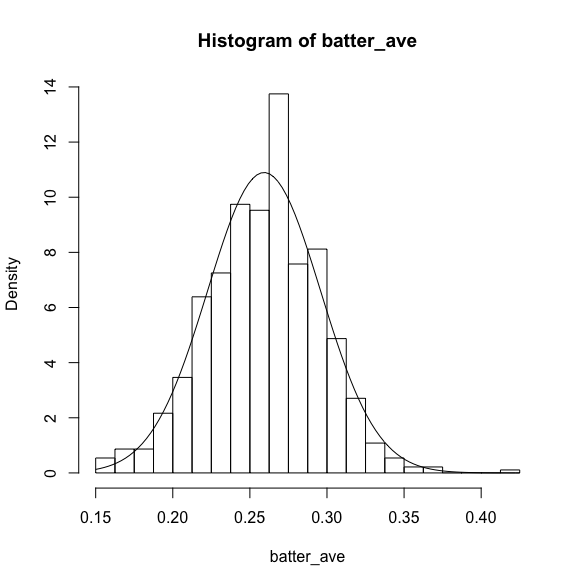
では、この値を先ほどのヒストグラムに追記して見ます。

> curve(dnorm(x, sd=sd(batter_ave), mean=mean(batter_ave)), add=TRUE)
---

このように、おおよそ打率の分布は正規分布と似通っていることが分かりました。

続いて、HRについてみてみましょう。
batter_HRには同様の期間の各打者のHRが格納されています。

> head(batter_HR);length(batter_HR)
[1] 12 5 22 13 7 22
[1] 739

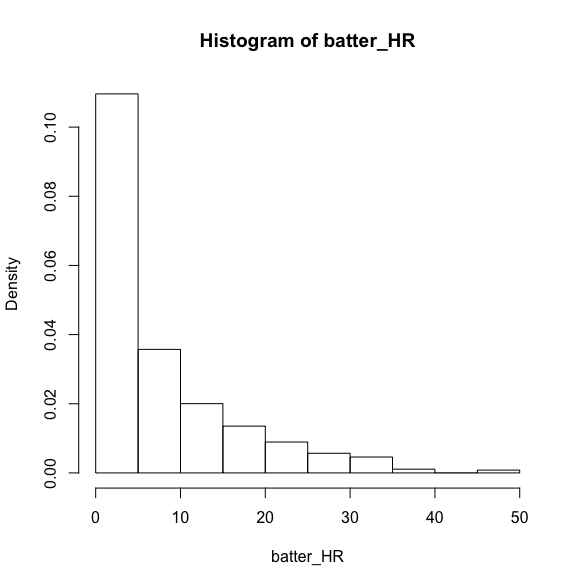
ヒストグラムを確認してみます。

> hist(batter_HR, freq=FALSE, seq(0,50,5))
---

先ほどとは異なり、右肩下がりのグラフとなります。
比べるまでもないですが、正規分布のグラフを重ねてみます。
まずは、平均値と標準偏差を確認します。

> mean(batter_HR)
[1] 8.102842
> sd(batter_HR)
[1] 8.696025

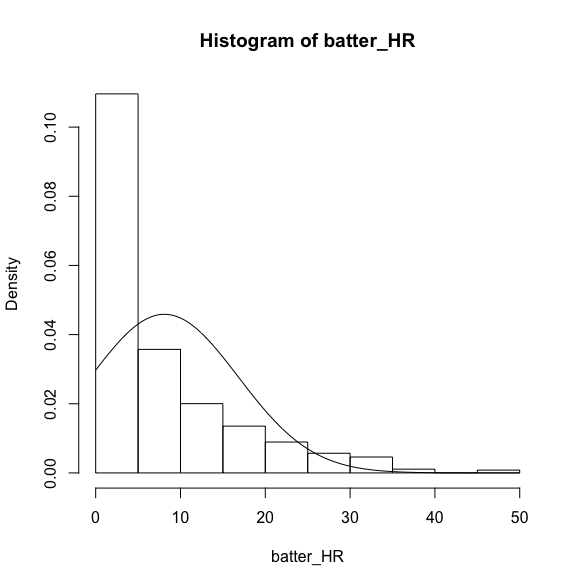
同様に、先ほどのグラフに正規分布のグラフを重ねます。

> curve(dnorm(x, sd=sd(batter_HR), mean=mean(batter_HR)), add=TRUE)
---

一見すると似てなくもないですが、~10までの範囲では全く異なる結果となります。

このように、打率は正規分布に沿いますが、HRはあまり沿わないことが分かりました。

正規分布は様々な統計処理で扱われる基本的な値ですが、今回ご紹介したようにデータによって分布が正規分布に沿わない場合もあります。
ヒストグラムなどでデータの分布をまずは確認するようにしましょう。

以上、ありがとうございました。