R言語での、標準化について紹介します。
以下で使用するデータは、batter_YY にYY年の打者成績が入っています。
※使用するデータはすべてプロ野球データFreak様からお借りしています。
プロ野球データFreak
スポンサーリンク
~目次~
1. 標準得点(z得点)
2. 偏差値
3. 変動係数
1. 標準得点(z得点)
標準得点とは、データ群の平均値と標準偏差がある特定の値になるように標準化された得点のことをいいます。
このうち、平均値を0、標準偏差を1になるように変換した標準得点をz得点といいます。
z得点の定義式は以下になります。
z得点 = (データの値 - 平均) / 標準偏差
この式は、例えば素点が平均 + 標準偏差の人のz得点は"1"であることが分かります。
つまり、標準得点は平均から標準偏差いくつ分離れているかを示しているとも言えます。
データを含む配列を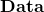 とすると、
とすると、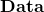 のx番目の人のz得点は、Rでは以下のように求められます。
のx番目の人のz得点は、Rでは以下のように求められます。
配列 <- データを格納
z得点 <- (配列[x] - mean(配列) ) / sqrt(mean((配列 - mean(配列))^2))
※配列[x]は、配列のx番目の要素をさす
なお、sqrt( mean ( (配列 - mean(配列) )^2 ) )の部分では標準偏差を求めていますが、これはsd(配列)とは異なることに注意してください。
sdを使いたい場合は、以下になります。
これは、sdは不偏分散から導出された標準偏差を使用しており、要素数nを一つ減らして計算されるためです。
詳細はこちらをご参考下さい。
z得点 <- (配列[x] - mean(配列) ) / ( sd(配列) * sqrt((n-1) / n) )
※nは配列の要素数length(n)
以下に具体例を示します。
> (batter_17
![Rendered by QuickLaTeX.com 打点[1] - mean(batter_17](http://by-oneself.com/wp-content/ql-cache/quicklatex.com-5678c50df6a00219ce5104166d593f59_l3.png)
打点)) / sqrt(mean((batter_17
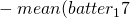
打点))^2))
[1] -0.4606066
上記では、打率が1位の選手(batter_17![Rendered by QuickLaTeX.com 打点[1])の打点について、z得点を表示しています。 z得点は平均を0としているので、平均より低いことがわかります。 これは、打率でいうと以下のように、0.237の打率の人と同じ程度の打点である、という事ができます。 <div class="graybox">> (batter_17](http://by-oneself.com/wp-content/ql-cache/quicklatex.com-b4b1ceaabb331d9d3e539518b8493aa9_l3.png) 打率[52] - mean(batter_17
打率[52] - mean(batter_17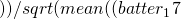 打率 - mean(batter_17
打率 - mean(batter_17![Rendered by QuickLaTeX.com 打率))^2)) <span class="rmarker">[1] -0.441253</span> > batter_17](http://by-oneself.com/wp-content/ql-cache/quicklatex.com-2cf0fb415e65bb2f1cfc115922c5a253_l3.png) 打率[52]
打率[52]
[1] 0.237
このように、打率と打点という二つのものを比較できるのがz得点の特徴です。
ちなみに、sdを使った定義式でも、同様の値となることを確認できます。
> n <- length(batter_17
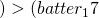
打点[1] - mean(batter_17
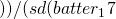
打点) * sqrt((n-1)/n))
[1] -0.4606066
2. 偏差値
偏差値とは、テストなどでよく出てくる平均点の人が50となる指標です。
実は、これはz得点と類似した指標で、以下の式で定義されます。
偏差値 = z得点 * 10 + 50
z得点の定義が平均0、標準偏差1だったので、これはデータを平均50、標準偏差10で変換していることを意味します。
先ほどのべた標準得点と同様に、偏差値は素点(標準化されていない元の値)が平均より標準偏差だけ上回れば偏差値が10上がる(素点が"平均+標準偏差"の人は、偏差値60)と言えます。
Rでは以下のように計算できます。
偏差値 = ( (配列[x] - mean(配列) ) / sqrt(mean((配列 - mean(配列))^2)) ) * 10 + 50
具体例として、2017年の打率上位5位の偏差値を求めてみます。
> (batter_17
![Rendered by QuickLaTeX.com 打率[1:5] - mean(batter_17](http://by-oneself.com/wp-content/ql-cache/quicklatex.com-1d0d849b665b049e679305bbdb2fbdca_l3.png)
打率)) / (sd(batter_17
![Rendered by QuickLaTeX.com 打率) * sqrt((n-1)/n)) * 10 + 50 [1] <span class="hutoaka">91.19762</span> 70.20658 67.61510 64.76446 64.50532 > batter_17](http://by-oneself.com/wp-content/ql-cache/quicklatex.com-65003df6aa6e4ae685ad3561a7e954cf_l3.png)
打率[1:5]
[1]
0.413 0.332 0.322 0.311 0.310
なんと、打率1位の近藤選手の打率の偏差値は90を超えています。
殆どの人は自分のテストで90を超える偏差値は見た事がないかと思います。
打率4割のすごさが分かりますね。
3. 変動係数
変動係数とは、標準化された標準偏差のことをいいます。
定義は以下になります。
変動係数 = 標準偏差 / 平均
Rでは以下のように求められます。
変動係数 = sd(配列) / mean(配列)
この値は、データ間の標準偏差を平均値の大きさの影響を受けずに比較するために使用されます。(例えば単位の違う値など)
そもそも、標準偏差(及び分散)は値の大きさの影響を受けるため、平均が異なるもの同士で分散の大きさを比較する事ができません。
例えば、以下のように配列1と配列1を2倍した配列2について、標準偏差を求めると、標準偏差も2倍になっている事がわかります。
> 配列1 <- c(1,2,3,4)
> 配列2 <- c(2,4,6,8)
> sd(配列1)
[1] 1.290994
> sd(配列2)
[1] 2.581989
これらを平均で割る事で変動係数が求められます。配列1と配列2で同じ値になっている事がわかります。
> sd(配列1) / mean(配列1)
[1] 0.5163978
> sd(配列2) / mean(配列2)
[1] 0.5163978
実際のデータで確認してみます。
打率と本塁打率(本塁打数/打数)のどちらの方がよりばらつきが大きいかを調べるために、標準偏差を計算します。
> HIT_rate <- batter_17

本塁打 / batter_17$打席数 > sd(HIT_rate)
[1] 0.03885131
> sd(HR_rate)
[1] 0.01946687打率の方が本塁打率よりばらつきが大きいように見えます。
しかし、ヒストグラムを見てみると、明らかに打率の方が平均近辺にデータが密集しており、ばらつきは小さいように見えます。

そこで、変動係数を調べてみると、以下のように本塁打率の方が5倍以上ばらつきが多い事がわかります。
> sd(HIT_rate) / mean(HIT_rate)
[1] 0.1529416
> sd(HR_rate) / mean(HR_rate)
[1] 0.815261
このように、変動係数を調べる事で、平均値の違う値についても正確に分散の比較ができる事がわかりました。
以上です。
![]() とすると、
とすると、![]() のx番目の人のz得点は、Rでは以下のように求められます。
のx番目の人のz得点は、Rでは以下のように求められます。![]() 打率[52] - mean(batter_17
打率[52] - mean(batter_17![]() 打率 - mean(batter_17
打率 - mean(batter_17![]() 打率[52]
打率[52]