離散型の確率分布であり、二項分布の特別な場合の分布であるポアソン分布の概要や使い方についてまとめました。
二項分布はこちら:【R言語と統計の備忘録】二項分布のまとめ
~目次~
1. ポアソン分布の概要
ポアソン分布は、二項分布においてn(試行回数)が大きく、p(成功(発生)確率)が小さい場合の分布です。
ポアソン分布では、このnとpをまとめて![]() とおき、一定の事象数や時間あたりの発生件数として使用します。
とおき、一定の事象数や時間あたりの発生件数として使用します。
例えば、1年間の10万人あたりの交通事故の件数や、一定時間に窓口を訪れる人の数などが当てはまります。
他には、経済学者であるボルトキーヴィッチが馬に蹴られて死んだ兵士の数の規則性を発見した話が有名です。
この馬に蹴られて死んだ兵士の話を、上記のnとpに当てはめると以下になります。
n: 兵士の数
p: 1回の出撃時に、兵士が馬に蹴られて死ぬ確率
f(x): 死んだ兵士の数がx人である確率(P(X=x))
2. ポアソン分布の確率密度関数
ポアソン分布の確率密度関数は以下になります。
このように、ポアソン分布は![]() のみに依存する分布となっています。
のみに依存する分布となっています。
例題を解いてみましょう。
![]() を代入します。
を代入します。
![]() 約
約![]()
※0!=1となります。
約13.5%となりました。つまり、ほぼ毎月不良品は出るもの、と思っていた方が良いということになりますね。
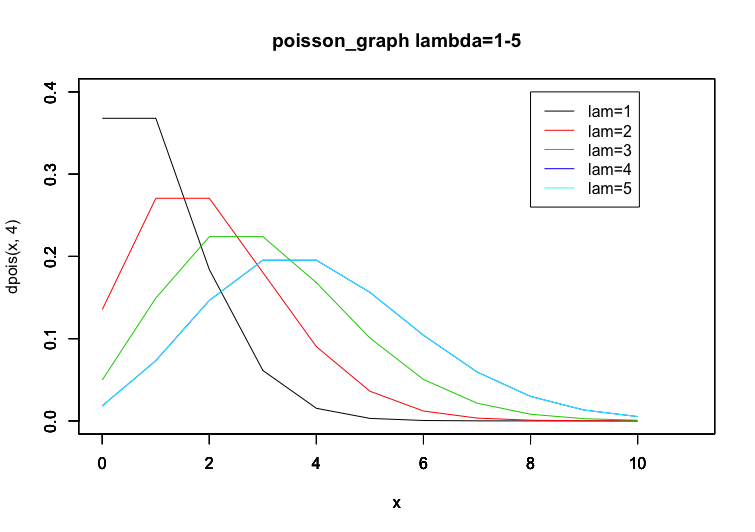
参考に、様々な![]() での確率分布関数を以下に示します。
での確率分布関数を以下に示します。
3. ポアソン分布の期待値と分散の導出
ポアソン分布の期待値と分散は以下になります。
この期待値![]() は、二項定理の期待値
は、二項定理の期待値![]() と同様であることは理解しやすいかと思います。
と同様であることは理解しやすいかと思います。
また、分散![]() についても、二項定理の分散
についても、二項定理の分散![]() において、p→0の時に同等となることが分かります。
において、p→0の時に同等となることが分かります。
期待値と分散からも二項分布と同等であることが分かります。
それぞれの計算方法は以下になります。
ポアソン分布の期待値の導出
次に上記の確率分布関数から期待値を求めます。
![]() ・・・期待値の公式より
・・・期待値の公式より
![]()
![]()
![]() ・・・
・・・![]() とする
とする
ここで、![]() は、
は、![]() の公式そのものであるため、値を代入する。
の公式そのものであるため、値を代入する。
![]()
![]()
ポアソン分布の分散の導出
以下の公式を使います。
![]()
まずは、上式の左項![]() を求めます。
を求めます。
![]() ・・・期待値の公式より
・・・期待値の公式より
![]()
![]()
![]() ・・・
・・・![]() とする
とする
![]()
ここで、まずは左項![]() を計算します。
を計算します。
![]()
![]()
![]() ・・・
・・・![]() とする
とする
![]() ・・・マクローリン展開の公式より
・・・マクローリン展開の公式より
![]()
続いて、右項![]() を計算します。
を計算します。
![]()
![]() ・・・マクローリン展開の公式より
・・・マクローリン展開の公式より
![]()
以上から、以下が導出できました。
![]()
最後に、![]() に代入します。
に代入します。
![]()
![]()
![]()
以上となります。
4. ポアソン分布の期待値と分散の導出(モーメント)
続いて、モーメント(積率母関数)を用いて期待値と分散を導出します。
モーメント関数の定義および公式は以下になります。
ポアソン分布のモーメント母関数
まず、ポアソン分布のモーメント母関数を求めます。
![]()
・・・3章と同様に、![]() より
より
![]()
![]()
ここで、![]() のマクローリン展開より、
のマクローリン展開より、![]() とすると
とすると
![]()
![]()
ポアソン分布のモーメント母関数の1回微分と期待値
1-p=qと置くと、モーメント母関数の1回微分は以下になります。
![]()
以上から、期待値は以下になります。
![]()
ポアソン分布のモーメント母関数の2回微分と分散
同様に、2回微分は以下になります。
![]()
以上から、分散は以下になります。
![]()
5. ポアソン分布のRでの扱い方
xを指定した時の事象の発生確率(dpois)
ポアソン分布をRで導出するにはdpois関数を使用します。
使い方は以下になります。
==================
dpois(x, ![]() )
)
x:成功(発生)回数
==================
![]() を代入します。
を代入します。
[1] 0.1353353
成功回数がn以上(累積分布)となる確率(ppois)
n個以上となる方法を求める場合はppois関数を使います。
パラメータの入れ方はdpois関数と同じになります。
ただし、ppois関数はn回以下となる確率なので注意しましょう。
以下の例題を解いてみます。
3個以下となる確率はppois(3,2)となるので、4個以上となる確率は以下になります。
[1] 0.1428765
上記はdpois関数を使用して以下でも求められます。(不良品の個数が0個, 1個, 2個, 3個の確率を全て足しています)
[1] 0.1428765
確率qで、成功回数がx回以下となるxの値(分位関数)を求める方法(qpois)
これはppois関数の逆関数になります。
別の言い方をすると、成功回数が0回からx回までの累積確率がqを超えない最大のxを返します。
==================
qpois(p, ![]() )
)
p:成功(発生)回数がx回以下となる確率
==================
以下の例題を解いてみます。
つまり、不良品の個数がx個以下となる確率pが、11/12を上回る確率を求めます。
算出方法は以下になります。
[1] 4
以上から、品質目標は一月の不良品4個とすれば良いことが分かります。
(ただし、あくまで確率なので、4個を超える可能性は十分にあります)
では、4個以下となる確率を念のため求めましょう。
[1] 0.947347
4個以下となる確率は、約95%となることから、11/12=約92%を上回ることが確認できました。
二項分布の乱数の出力(rpois)
二項分布の乱数はrbinom関数で出力できます。
使い方は以下になります。
==================
rpois(n, ![]() )
)
n:乱数の個数
==================
以下の例題を出してみましょう。
以下のようになります。
※結果は毎回変わります
[1] 1 7 0 0 0 0 4 5 2 1 3 1
この年だと、先ほどの品質目標(4個を超える月は1月以下)を満たせませんね。
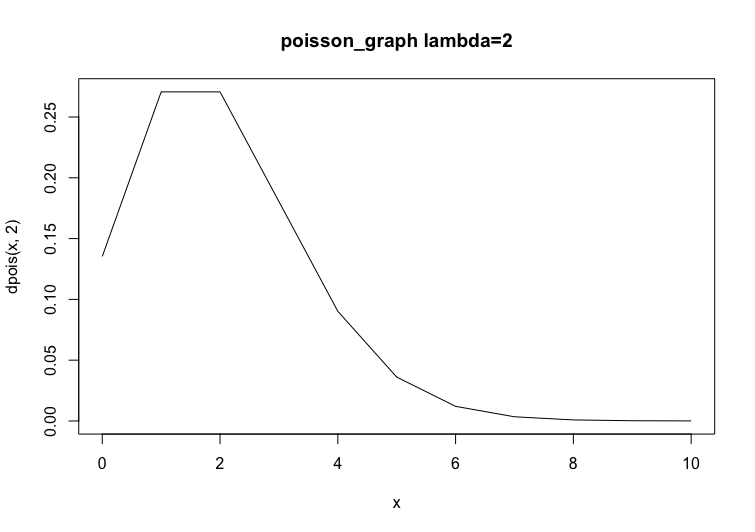
Rによる二項分布の確率分布関数と累積確率分布関数のグラフの書き方
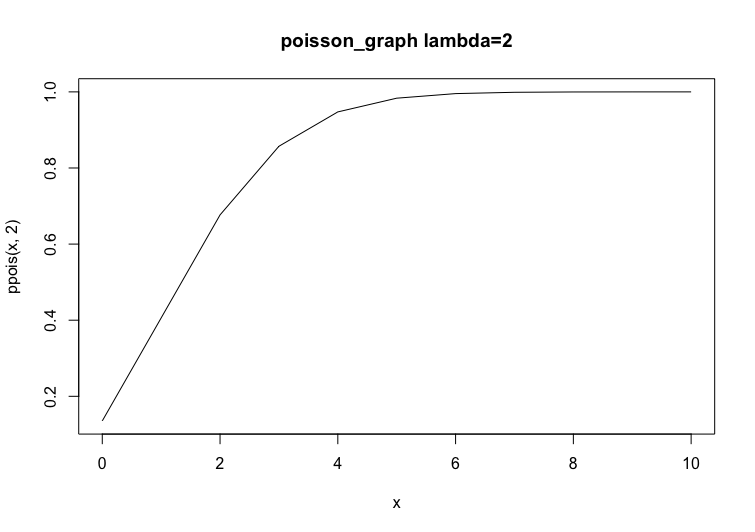
確率分布関数のグラフはdpoisを、累積分布関数のグラフはppoisを使います。
同様に、累積密度関数は以下になります。