離散型の確率分布であり、二項分布を拡張した分布の一つである幾何分布についてまとめました。
二項分布については以下を参照して下さい。
~目次~
1. 幾何分布の概要
幾何分布とは、成功(発生)確率がpの独立なベルヌーイ試行Tが初めて成功するまでの試行回数をxとし、x回目で初めてTが成功する確率の分布となります。
(二項分布はx回の試行において、独立なベルヌーイ試行Tが成功する回数がnとなる確率でした)
幾何分布となるものには、コイン投げや自動車事故など、同じ試行が何度も繰り返される時に初めて成功するまでの試行回数を分布したものがあります。
ちなみに、幾何分布(Geometric Distribution)の名前の由来は、以下で説明する確率変数![]() が等比数列(幾何数列)の形をしているからと言われています。
が等比数列(幾何数列)の形をしているからと言われています。
2. 幾何分布の確率密度関数
幾何分布の確率密度関数は以下になります。
p:成功(発生)確率
q:失敗確率(
x: 1回成功するまでの試行回数(成功した時を含む)
上記は、成功Tが1回発生するまでに、x-1回失敗していることから導出できます。
なお、成功数をn回とした時の分布を負の二項分布と言います。負の二項分布については以下を参照して下さい。
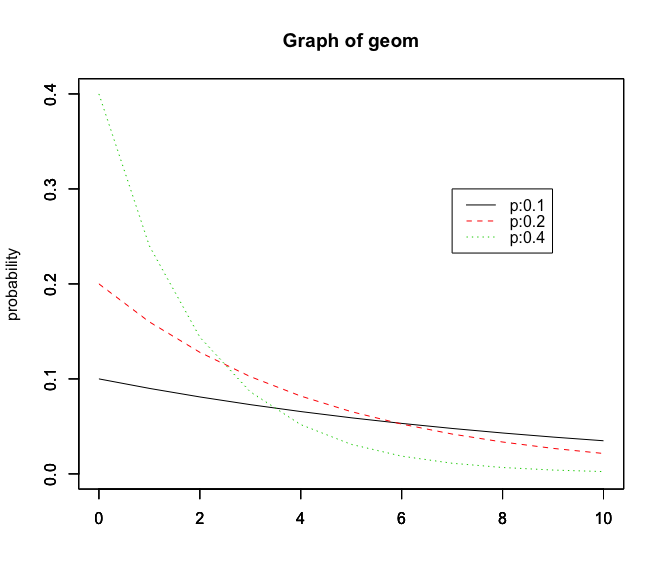
確率分布のグラフは以下になります。p=0.1,0.2,0.4のグラフになります。
例題を解いてみましょう。
ここで、ハートを引く=成功となりますので、![]() となります。
となります。
また、4回目で成功する確率を求めるので![]() となります。
となります。
以上から、約10.4%と求めることができました。
3. 幾何分布の期待値と分散(モーメント)
幾何分布の期待値と分散は以下になります。
幾何分布はモーメント(積率母関数)を用いて期待値と分散を導出します。
モーメント関数の定義および公式は以下になります。
幾何分布のモーメント母関数
まず、幾何分布のモーメント母関数を求めます。
![]() ・・・期待値の公式:
・・・期待値の公式:![]() のxに
のxに![]() を代入
を代入
![]()
![]()
ここで、無限級数の和の公式![]() より
より
![]()
![]()
幾何分布のモーメント母関数の1回微分と期待値
幾何分布のモーメント母関数の1回微分は以下になります。
![]()
![]() ・・・
・・・![]() より
より
以上から、期待値は以下になります。
![]()
幾何分布のモーメント母関数の2回微分と分散
同様に、2回微分は以下になります。
![]()
![]()
以上から、分散は以下になります。
![]()
![]()
![]()
![]()
以上になります。
4. 幾何分布のRでの扱い方
xを指定した時の事象の発生確率(dgeom)
幾何分布をRで導出するにはdgeom関数を使用します。
使い方は以下になります。
x:初めて成功するまでに失敗した回数
p: 成功確率
xが"失敗した回数"であることに注意して下さい。
3回目に成功する確率が知りたいときはx=2を代入します。
例題を解いてみましょう。
ここで、p=0.25, x=3より以下になります。
[1] 0.1054688
2章で手計算で計算した時と同じ結果を得ることができました。
成功回数がn以上(累積分布)となる確率(pgeom)
n個以上となる方法を求める場合はpgeom関数を使います。
パラメータの入れ方はdgeom関数と同じになります。
例題を解いてみましょう。
ここでもxは失敗した回数であることに注意して下さい。
p=0.25, x=2より以下になります。
[1] 0.578125
別の言い方をすると、「ハートを引くまでカードを引くゲームをした時に、ハート以外を引く回数が2回以下である確率は0.578である」
これは、dgeomで1回目,2回目, 3回目に成功する3回の総和に等しいことを確認します。
[1] 0.578125
以上になります。
確率qで、成功回数がx回以下となるxの値(分位関数)を求める方法(qgeom)
これはpgeom関数の逆関数になります。
別の言い方をすると、初めて成功するまでの失敗回数が、x回以下である確率がPを超える最小のxを返します。
使い方は以下になります。
P: 累積確率
p: 成功確率
例題で見てみましょう。
挑戦者の50%以上がハートを引くには、最低何回カードを引くことにすれば良いか。
上記のqgeom関数にそのまま代入します。
[1] 2
上記の結果は、50%以上の確率で2回までの失敗に収まる、という結果となるため、3回カードを引くことにすれば良いことが分かります。(2というのはあくまで失敗回数のため)
幾何分布の乱数の出力(rgeom)
幾何分布の乱数はrgeom関数で出力できます。
使い方は以下になります。
n:1回成功するまでに失敗する数
p: 成功確率
例題で見てみましょう。
上記のrgeom関数にそのまま代入します。
[1] 2 4 1 16 5 3 11 1 6 4 13 2 2 3 2 1 3 2 2 3
rgeomだけでは失敗した回数しか出ないので+1しています。
こう見ると、個人的には結構ばらつきが多いと感じますがみなさんはいかがでしょう。
Rによる二項分布の確率分布関数と累積確率分布関数のグラフの書き方
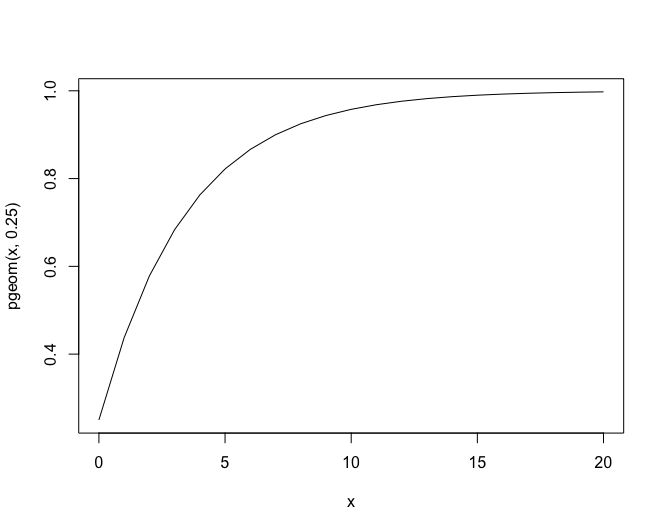
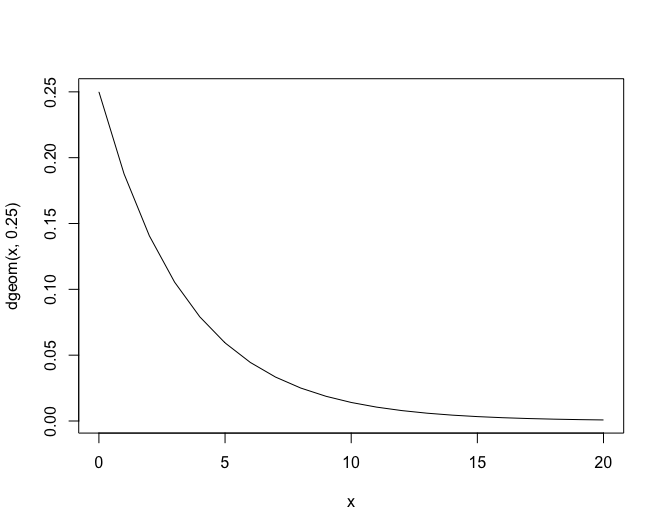
確率分布関数のグラフはdgeomを、累積分布関数のグラフはpgeomを使います。
> x <- c(0:20)
> plot(x, pgeom(x, 0.25), type="l")