分散の公式について、その証明と具体例をご紹介します。
(分散の導出及び、分散の式変形に関する公式です)
~目次~
1. [基本]分散の導出公式
確認のため、分散の公式を記載します。
公式
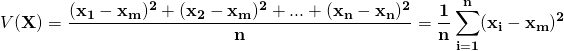
#不偏分散の場合
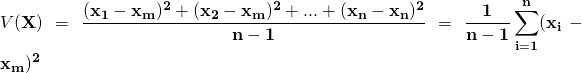
具体例を用いた確認
Rを用いて、実際に計算してみます。
> V_X <- ( (X[1] - mean(X))^2 + (X[2] - mean(X))^2 + (X[3] - mean(X))^2 +(X[4] - mean(X))^2 +(X[5] - mean(X))^2) / 5
> V_X
[1] 2
Rにはvarという関数がありますので、こちらを使用して求めてみます。
[1] 2.5
varは、不偏分散を導出しているため、![]() をかけます。(今回要素数n=5)
をかけます。(今回要素数n=5)
[1] 2
公式を用いた計算結果と同じになることが確認できました。
2. 全てのデータをa倍した場合の分散
全てのデータをa倍した場合の分散は、a^2倍されます。
公式
![]()
※![]() は
は![]() の分散、
の分散、![]() は対象のデータ配列、
は対象のデータ配列、![]() は定数
は定数
証明
標本データ![]() を以下とします。
を以下とします。
![]()
![]() の分散
の分散![]() は
は![]() の平均を
の平均を![]() とすると以下になります。
とすると以下になります。
![]()
同様に、![]() に定数aをかけた
に定数aをかけた![]() を以下とします。
を以下とします。
![]()
![]() の分散
の分散![]() は以下になります。
は以下になります。
![]()
=![]()
=![]()
=![]()
=![]()
以上です。
具体例を用いた確認
先ほどと同様に![]() とその分散
とその分散![]() を以下とします。
を以下とします。
[1] 1 2 3 4 5
> a
[1] 2
> var(X)
[1] 2.5
定数aを2とすると、その分散が![]() となることが確認できました。
となることが確認できました。
[1] 10
> a^2 * var(X)
[1] 10
3. 全てのデータにaを足した(データの平均をx移動させた)場合の分散
全てのデータに定数を足した場合でも、分散には影響がありません。(平均値の変動は分散には影響しない)
公式
![]()
※![]() は
は![]() の分散、
の分散、![]() は対象のデータ配列、
は対象のデータ配列、![]() は定数
は定数![]() の配列
の配列
スポンサーリンク
証明
標本データ![]() と定数ベクトル
と定数ベクトル![]() を以下とします。
を以下とします。
![]()
![]()
![]() は
は![]() の平均は
の平均は![]() となることから以下となります。
となることから以下となります。
![]()
=![]()
=![]()
=![]()
具体例を用いた確認
a=2の時、![]() は以下となります。
は以下となります。
[1] 3 4 5 6 7
![]() と
と![]() の分散をそれぞれ求めると、同じとなることが分かります。
の分散をそれぞれ求めると、同じとなることが分かります。
[1] 2.5
> var(X+a)
[1] 2.5
4. 独立した二つのデータを足した場合の分散
二つの独立したデータの分散の和は、それぞれの分散の和と等しくなります。
公式
![]()
※![]() は
は![]() の分散、
の分散、![]() と
と![]() は対象のデータ配列
は対象のデータ配列
導出方法
二つの独立した標本データ![]() と
と![]() を以下とします。
を以下とします。
![]()
![]()
![]() の平均を
の平均を![]() 、
、![]() の平均を
の平均を![]() とすると、
とすると、![]() は以下になります。
は以下になります。
![]()
=![]()
ここで、![]() を以下のように展開します。
を以下のように展開します。
![]()
=![]()
![]()
=![]()
ここで上式の第1項は![]() 、第2項は
、第2項は![]() となります。
となります。
また、第3項は![]() より、0となります。
より、0となります。
以上から、以下が導出されました。
![]()
具体例を用いた確認
Rを使用して、具体例で確認します。
![]() と
と![]() を以下で作成します。
を以下で作成します。
rnorm(n, mean, sd)は、は平均"mean"で標準偏差が"sd"の乱数を"n"個作成します。
以下では、平均0で標準偏差が1(分散は1)の乱数を1000個と、平均0で標準偏差が3(分散は9)の乱数を1000個作成します。
乱数ができているかを、確認します。最初の5個だけみてみます。
[1] -1.8922349 -1.0520299 0.4780840 -0.6979630 -0.5113521 -0.6088880
> head(Y)
[1] -3.8676957 5.8847385 -1.2284424 -0.8252495 2.2898359 -3.2330217
できましたので、それらの合計の分散と、個々の分散の合計を求めます。
[1] 10.52636
> var(X) + var(Y)
[1] 10.59839
このように、それらの合計の分散と個々の分散の合計は、ともに約10となることが確認できました。
ちなみに、"独立でない"とは片方のデータがもう片方のデータと関係性があるという意味になります。
独立でない乱数同士を足すと以下のように公式を満たさないことがわかります。
>Y <- X*3+2
> var(X+Y)
[1] 15.6313
> var(X) + var(Y)
[1] 9.769559
5. 分散のもう一つの導出方法
1.で紹介した方法以外にも、データの個々の二乗の平均からデータ全体の平均の二乗を引いても導出できます。
使用機会は多いので、こちらも使えるようにしておきましょう。
公式
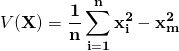
スポンサーリンク
導出方法
上記の公式は、1.でご紹介した基本の公式から導出します。
![]()
=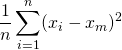
=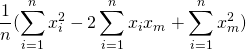
ここで、![]() の中にある定数は外に出します。
の中にある定数は外に出します。
=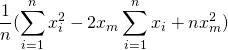
また、データの総和と平均を要素数でかけたものは等しいことから、![]() と変換します
と変換します
=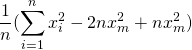
=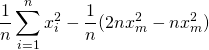
=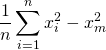
以上です。
具体例を用いた確認
分散を求めるXを以下とします。
今回の公式の方法で分散を求めると、以下となります。
ここで、![]() を
を![]() の平均として計算しています。
の平均として計算しています。
[1] 1 4 9 16 25
> mean(X^2) - mean(X)^2
[1] 2
※mean(X)は配列Xの平均を出力します
一方で、1.でご紹介した公式で求めた分散は以下となります。
> var_X
[1] 2
※length(X)はXの要素数(n)を出力します。今回は5となります。
なお、Rには分散を求めるvarがあるため、そちらでも確認します。
(varは不偏分散のため、![]() をかけて分散に変換しています。)
をかけて分散に変換しています。)
[1] 2
いずれの方法でも、2となることが確認できました。