R言語での、2変数以上の統計値の取り扱いについて紹介します。
以下で使用するデータは、batter_YY にYY年の打者成績が入っています。
※使用するデータはすべてプロ野球データFreak様からお借りしています。
プロ野球データFreak
スポンサーリンク
~目次~
1. 散布図(plot)の基本と頻出オプション
散布図の基本
2変数統計量の説明に入る前に、2変数の統計量を見る時に非常に大事な散布図の書き方と良く使用するオプションについてご紹介します。
散布図は、x軸とy軸に異なる変数を対応させデータをプロットした図になります。
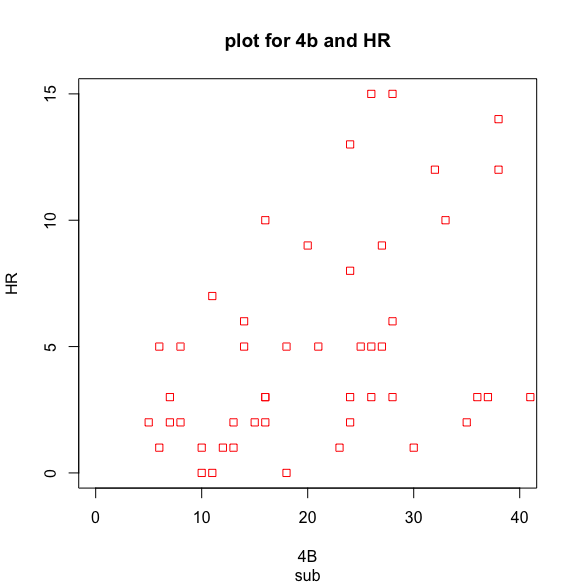
まずは見ていただいた方が早いと思うので、以下に2017年の打率と本塁打の相関を記載します。
なんとなく、右上に伸びているのが分かりますね。一方で、本塁打(y軸)の値が低い(1桁)の場合は、そこまで相関が無いように見えます。
こういった全体的な傾向を一目で把握できるので、2変数のデータを与えられたらまずは散布図を見て見ましょう。
(列名が日本語のため、文字化けしています)
散布図でよく使用するオプション
・データの範囲を指定:xlim=c(x_min, x_max), ylim=c(y_min, y2_max)
・プロットする点の形状を指定:type="**"
**にはp(点), l(線), b(点と線), h(各プロットからx軸への垂線)などがあります。
・プロットする点の色を指定:col=num
numには1(黒), 2(赤), 3(緑), 3(青)などが入ります。
・ラベルの記載
・main="メインタイトル"
・sub ="サブタイトル"
・xlab="Xラベル",ylab="Yラベル"
実際にオプションをつけると、以下になります。
+ type="p", pch=0, col=2, #形状の指定
+ xlim=c(0,40), ylim=c(0,15), #範囲の指定
+ main="plot for 4b and HR", sub="sub", xlab="4B", ylab="HR" #表記の指定
+ )
2. 共分散
共分散は二つの値の間の相関の強さを調べる変数となります。
あとで説明する相関係数の方が有名ですが、相関係数の元となっているのが共分散です。
n個のデータをもつxとyの共分散は以下になります。
※x_m と y_m はそれぞれxとyの平均を示す。
Rでは以下になります。
ただし、covで求められるのは"不偏共分散"であり、共分散の最後に n で割る代わりに n-1 で割ります。
なぜこのような"不偏"分散となっているかは、下記もご参考ください。
では実際に求めて見ましょう。
先ほどplotで相関がありそうだと思われる本塁打と打点の共分散は以下になります。
[1] 122.0148
約122という値が出ました。
実は、共分散には指標として一つ問題点があります。
それは、ベースとなる値によって関係性が同じでも値が変動してしまいます。
例えば、以下のように片方の値を10倍すると、以下のように共分散の値も10倍になります。
このように、単位などが異なるだけで値が変わるため、相関があるのか無いのか、強いのか弱いのか、が分かりません。
[1] 1220.148
この欠陥を無くしたのが次に説明する相関係数になります。
3. 相関係数
先に説明した共分散の欠点を排除したのが相関係数(correlation coefficient)になります。(正確にはピアソンの積率相関係数と言います。)
相関係数は-1から1の間の数を取り、1に近ければ正の相関(片方が大きくなれば、もう片方も大きくなる)を持ちます。
また、-1 に近ければ、負の相関(片方が大きくなれば、もう片方は小さくなる)を持ちます。
定義は以下になります。
Rで求める際は以下になります。
= cov(x, y) / (sd(x) * sd(y))
実際に求めて見ましょう。
先ほどと同様に、本塁打と四球の相関係数を求めます。
[1] 0.6355266
また、二つ目の定義式でも同様に求められます。
[1] 0.6355266
約0.64という値が出ました。
一般的に相関係数の大きさの目安として以下があります。
相関係数と相関の強さ
0.2 ~ 0.4:弱い相関
0.4 ~ 0.7:中程度の相関
0.7 ~ 1.0:強い相関
今回の0.64という値は、中程度の相関があるということが分かりますね。
念のため、相関係数の値が、共分散のネックであったデータ値の大きさで変わることが無いか確認します。
[1] 0.6355266
このように、データの大きさに左右されないことが分かりました。
(参考)色々な相関係数のプロット
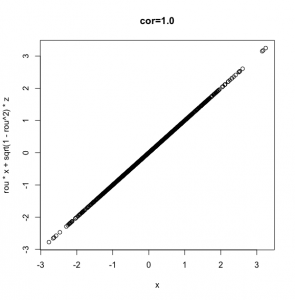
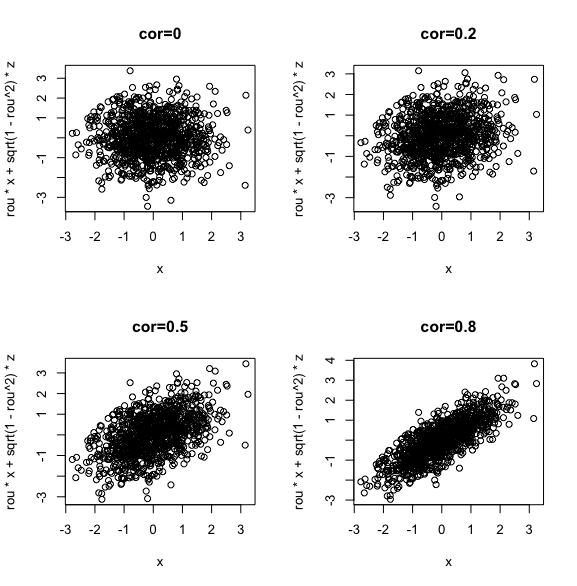
参考に、相関係数(ρ)=0/0.2/0.5/0.8/1でのプロットの結果を図示します。
イメージを掴んでみてください!
(参考の参考)相関係数を指定した乱数の出力
・独立で、平均と分散が同じ乱数x と zを作成する
・出力したい相関係数ρを決める
・y = ρ * x + √(1-ρ) * z を求める
・xとyが相関係数ρのペアとなる。
> z <- rnorm(1000)
> cor(x, rou*x + sqrt(1-rou^2) * z)
[1] 0.008939111
> plot(x, rou * x + sqrt(1-rou^2) * z)
> cor(x, rou*x + sqrt(1-rou^2) * z)
[1] 0.2014787
> plot(x, rou * x + sqrt(1-rou^2) * z)
> cor(x, rou*x + sqrt(1-rou^2) * z)
[1] 0.4922132
> plot(x, rou * x + sqrt(1-rou^2) * z)
> cor(x, rou*x + sqrt(1-rou^2) * z)
[1] 0.7912933
> plot(x, rou * x + sqrt(1-rou^2) * z)
> cor(x, rou*x + sqrt(1-rou^2) * z)
[1] 1
> plot(x, rou * x + sqrt(1-rou^2) * z)
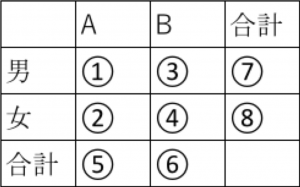
4. クロス集計表とファイ係数
最後にクロス集計表とファイ係数についてご紹介します。
この二つは、質的変数(連続した数字ではなく、○×等の変数)のデータを扱うときに使用されます。
クロス集計表
クロス集計表をRで作成するには、以下の式になります。
具体例を見て見ましょう。
2018年の打者データについて、西武の選手の場合は1, それ以外のチームの場合は0とします。
また、OPS(※)が7割りを超える打者を1, 7割を切る打者を0とします。
※OPSとはOn plus sluggingの略であり、出塁率と長打率を足した値。0.8を超えると一流、1.0を超えると超一流と言われている。
下準備として、以下の操作を行います。
これにより、チーム列が"西武"の場合は1を、それ以外の場合は0が格納されます。
また、OPSについても同様です。
[1] 0 1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[54] 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
> batter_18_OPS01 <- ifelse(batter_18$OPS > 0.7, 1, 0)
> batter_18_OPS01
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 0 0 1 1 0 0 0 0 1 0 1 1 1 1 0 0 0 0
[54] 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
それでは、集計して見ましょう。
batter_18_OPS01
batter_18_team01
-- 0 1
0 30 33
1 2 8
少し見辛いですが、例えば、両方0(西武の選手以外で、OPSが0.7未満)は30人いることが分かります。
このように質的変数の値を表にしたのがクロス集計表です。
ファイ係数
次に、ファイ係数について説明します。
ファイ係数は相関係数の特別な場合で、1と0の二つの値(二値変数)に対して計算される相関係数のことを言います。
(要素がn*nの場合(例えば6チームの各守備位置ごとの打率等)は、クラメールの連結関数で導出できますが、ここでは説明を省きます)
以下のように導出できます。
Rで求めるには以下になります。
見てわかる通り、相関係数と全く同じですね。
xとyにはクロス集計表と同様に1か0のみで作成された配列が入ります。(Aであるなら1、Bであるなら0などのように使用します)
先の例を元に、実際に計算して見ましょう。
[1] 0.1913868
このように、西武の選手であることとOPSが高いことはほとんど相関がありません。
しかし、クロス集計表をよく見てみると、西武以外の選手はOPS0.7以上と以下が半々なのに対し、西武の選手は8割がOPS0.7を超えています。
このように、相関係数自体は低くても、何かしらの関係がある場合があるので、相関係数だけでなく必ずクロス集計表(量的変数の場合は散布図)を見るようにしましょう。
以上です。