【R】lm()のsummary()の意味と導出方法【回帰分析】 | 世のため自分のためのアウトプット

lm()関数の備忘録です。
出力されている内容は概ね理解していたのですが、具体的にどうやって出すんだっけ？と思って調べたのでまとめておきます。

以下は、定番の赤本を参考にしました。
&lt;br /&gt;<br /><br />

手計算しやすいように例もとってもシンプル！


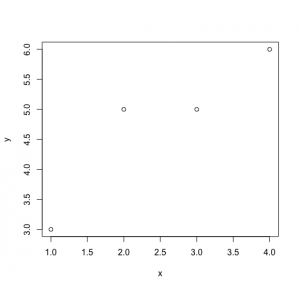
x <- c(1,2,3,4)
y <- c(3,5,5,6)
plot(x,y)

m <- lm(y ~ x)
summary(m)
Call:
lm(formula = y ~ x)

Residuals:
   1    2    3    4 
-0.4  0.7 -0.2 -0.1 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)   2.5000     0.7246   3.450   0.0747 .
x             0.9000     0.2646   3.402   0.0766 .
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.5916 on 2 degrees of freedom
Multiple R-squared:  0.8526,	Adjusted R-squared:  0.7789 
F-statistic: 11.57 on 1 and 2 DF,  p-value: 0.07662

とりあえず上から。

Residuals (残差)


Residuals:
   1    2    3    4 
-0.4  0.7 -0.2 -0.1

残差です。実際の値とモデルからの予測値との差
nの値が大きい(7以上の)時は、4分位数で表される。


y_pre <- predict(object = m, newdata = as.data.frame(x)) #予測値
Residuals <- y - y_pre
Residuals
[1] -0.4  0.7 -0.2 -0.1

Estimate


Coefficients:
            Estimate 
(Intercept)   2.5000
x             0.9000
---

最小自乗法での推定回帰係数の値。
ようは、 $y = \alpha x + \beta$ の $\alpha$ (上記出力ではx)と $\beta$ (同(Intercept))の値。数式で書くと以下になります。
$\alpha = \frac{\bar{\bf{y}}\sum_{i=1}^{n}\bf{x}_i - \sum_{i=1}^{n}\bf{x}\bf{y}}{\bar{\bf{x}}\sum_{i=1}^{n}\bf{x}_i-\sum_{i=1}^{n}\bf{x}_i^2}$
$\beta = \bar{\bf{y}} - \alpha \bar{\bf{x}}$
Rで出力すると、以下になります。


> alpha <- (mean(y) * sum(x) - sum(x*y))/(mean(x)*sum(x) - sum(x^2));alpha
[1] 0.9
> Intercept <- mean(y) - alpha*mean(x);Intercept
[1] 2.5

Residual standard error


Residual standard error: 0.5916 on 2 degrees of freedom

諸事情により、少し飛ばして2乗誤差。
モデルから求めた予測値と実際の値との差の二乗の合計です。
この値は何かというと、 $\alpha$ の標準偏差を、標本から推定したものになります(母分布の標準偏差は未知のため)。ようは不偏標準偏差です。


> se <- sqrt(sum((y_pre - y)^2)/(length(x) - 2));se
[1] 0.591608

"2 degrees of freedom"の2は自由度です。
今回は、要素数が4つに対して2つの制約があるので、自由度は以下になります。


> free_val <- length(x) - 2;free_val
[1] 2

Std. Error


Coefficients:
            Estimate Std. Error
(Intercept)   2.5000     0.7246
x             0.9000     0.2646

少し戻って、Interceptおよびalpha(xの係数)の標準誤差。検定に用いる(Interceptの方はあまり使わない)。
ようは、検定でよくやる標準化を実施したものです。数式を一応出しておきます。
(s.e.は、すでに導出したResidual standard errorのことです)
ここら辺のより詳しい解説は赤本の13章にしっかり書かれていますので、そちらを参照してください。
$s.e.(\hat{\alpha}} ) = \frac{s.e.}{\sqrt{\sum (\bf{X}_i - \bar{\bf{X}})^2}}$


> se.Intercept <- se *sqrt(sum((x)^2) / (length(x) * sum((x-mean(x))^2))); se.Intercept
[1] 0.7245688
> se.x <- se / sqrt(sum((x-mean(x))^2)); se.x
[1] 0.2645751

t value


Coefficients:
            Estimate Std. Error t value
(Intercept)   2.5000     0.7246   3.450
x             0.9000     0.2646   3.402

Interceptとxのt値です。
こちらも数式を書いておきます。 $\hat{\alpha}}$ は推定値で、ようは先ほど計算した0.9(Interceptの場合は2.5)が入ります。
$\alpha$ は帰無仮説での値である。この場合帰無仮説は「yをxで説明できない」となるため、0が入ります。
先ほど「Interceptの方はあまり使わない」と述べたのは、こっちの $\alpha=0$ に関する検定が主に行われるためです。
(ただし、lmでは両方の結果が出るので、両方計算しておきましょう。)
$t_2 = \frac{\hat{\alpha} - \alpha}{s.e.(\hat{\alpha})}$


> tval.Intercept <- (Intercept - 0) / se.Intercept; tval.Intercept
[1] 3.450328
> tval.x <- (alpha - 0) / se.x; tval.x
[1] 3.40168

Pr(>|t|)

このくくりの最後のp値です。


Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)   2.5000     0.7246   3.450   0.0747 .
x             0.9000     0.2646   3.402   0.0766 .

ここまででp値まで求めているので簡単ですね。
当然ですが両側検定(先ほど述べたように、0かどうかを検定しているため)です。
ptのデフォルトは片側検定のため、2倍して両側検定とします。
また、lower.tail = FALSEをつけないと、5%の値でなく95%ラインの値が出るので注意してください。


> pr.Intercept <- pt(tval.Intercept, df = 2, lower.tail = FALSE)*2; pr.Intercept
[1] 0.07470849
> pr.x <- pt(tval.x, df = 2, lower.tail = FALSE)*2; pr.x
[1] 0.07661948

Multiple R-squared<

決定係数と呼ばれるものです。


Multiple R-squared:  0.8526

目的変数の予測値が、どれぐらい対象となる変数(y)を説明しているかです。
例えば、テストの結果が前日の勉強時間と前回の点数のみで決まる場合(普通はありえまえんが)、前日の勉強時間のみでテストの結果を予測しようとすると、50%になります。(前日の勉強時間と前回の点数の重みが50:50の時)

こちらも数式を書いておきます。
$\eta^2 = \frac{\sum (\hat{\bf{y_i}} - \bar{y})^2}{\sum (\bf{y_i} - \bar{y})^2}$

数式を元に別の説明をすると、変動の総和は $\sum (\hat{\bf{y_i}} - \bf{y})^2$ で、xで説明できる変動は $\sum (\hat{\bf{y_i}} - \bar{y})^2$ であり、説明できない変動は $\sum (\hat{\bf{y_i}} - \bf{y_i})^2$ です。

今回は、85%を説明できていることから、大部分を説明できていることになります。


> Rsq <- 1 - sum((y_pre -y)^2)/sum((y-mean(y))^2); Rsq
[1] 0.8526316

なお、今回のように単回帰分析の場合は、相関係数からも求められます。


> cor(x,y)^2
[1] 0.8526316

F-statistic

最後に、F値になります。


F-statistic: 11.57 on 1 and 2 DF

これは、帰無仮説が「全ての因子は目的量(y)に対して効果がない」であり、対立仮説は「少なくても一つの因子は目的量(y)に対して効果がある」となります。
なお、これは通常単回帰分析では用いられません。なぜかというと、因子が一つであり、その因子に対する優位性のt検定を実施しているからです。
そのため、xのp値とF検定のp値が同じ値となっています。
$F = \frac{(S_0 - S_1)/p}{S_1/(n-k)}$
ここで、 $S_0$ は回帰残差の平方和であり以下である。
$S_0 = \sum \hat{e}_i^2 = \sum (\bf{y}_i - \bar{\bf{y}})^2$


> S_0 <- sum((y-mean(y))^2)
> S_1 <- sum((y_pre -y)^2)
> p <-1 #因子の数 単回帰分析の場合は1
> n <- length(y) #要素数
> k <- 2 #自由度
> F_val <- ((S_0 - S_1)/p) / (S_1 / (n-k)); F_val
[1] 11.57143

終わりに

備忘録なのにとても長くなりました。
全てを参照する方はいないと思いますが、何かのお役に立てれば幸いです。
疲れた。。