代表的な統計的仮説検定のt検定について、その概要とR言語を用いた具体的な検定方法についてご紹介します。
以下で使用するデータは、batter_YY にYY年の打者成績が入っています。
※使用するデータはすべてプロ野球データFreak様からお借りしています。
～目次～
１. t検定の概要と代表的なt検定
t検定は、統計的仮説検定の一つであり、日本工業規格では「検定統計量が，帰無仮説の下でt分布に従うことを仮定して行う統計的検定。」と定義されています。
また、母集団の分散(母分散)は不明であるが、分布は正規分布に従うと想定される際に使用されます。
t検定の種類としては、以下のようなものが代表的なものとして挙げられます。
今回は、この中の一群のt検定について説明します。
- 一群のt検定・・・標本データと母集団の標本統計量に有意な差があるかどうかを検定
- 回帰分析の係数・・・ある２群の標本データについて、それらの母集団の相関係数が、想定される値と等しいかどうかを検定
- 独立二群の平均値の差の検定・・・ある独立な２群の標本データについて、それらの母集団の平均値が等しいかどうかを検定
- 関連二組の差の平均値のt検定・・・ある関連のある２群の標本データについて、それらの標本統計量の差がある値に等しいかどうかを検定
※標本統計量・・・標本データの統計量(平均/分散等)
※独立な・・・二つのデータの間に関連性がないと想定されるもの。
例：全国の小学生を無作為に二つに分けた場合の、それらのグループの試験の得点等
※関連のある・・・二つのデータの間に関連性があると想定される場合。
例：あるグループの試験勉強前後の試験の点数/野球における本塁打と打点等
２. t検定の手順
t検定の手順は統計的仮説検定と同様になります。
統計的仮説検定の詳細は【R言語と統計の備忘録】統計的仮説検定も参照ください。
統計的仮説検定の手順
1. ある事象について、検定したい仮説(帰無仮説)を決める
2. 仮説を検定するための検定統計量を選択する
3. 検定の判断基準(有意水準)を設定する(現実的に起こりうるものかどうかの基準)
4. 今回の事象に対する検定統計量を計算(実現値)し有意水準と比較することで、仮説の正否を判断する。
３. t検定の具体例~2018年の西武打線の出塁率~
2018年のパリーグは、西武ライオンズが優勝しました(CSではソフトバンクに負けてしまいましたが。。)
特に話題になったのが山賊打線と呼ばれる西武打線です。
そこで、西武打線は統計的に見ても凄かったのか、それともまぐれなのか確認して見たいと思います。
今回は得点との相関が大きいと言われている出塁率に注目して検定を行います。
3章では、t検定の流れを理解するために、定義に沿って愚直にt検定を行います。
Rでt検定用の関数を使用して、簡単に行う方法を知りたい方は、4章をご覧ください。
早速t検定を行なっていきます。
0. 検定を行う前に
検定を行う前に、今から検定を行うデータの概要を把握しておきましょう。
以下はbatter_18というデータフレーム に、2018年パリーグの規定打席1/3以上の打席に立った打者の全てのデータが入っています。
まずは、データの概要です。summary関数で確認します。
少し見辛いですが、平均が0.323 最大値が0.431であることがわかりました。
> summary(batter_18$出塁率)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.2550 0.2930 0.3230 0.3228 0.3460 0.4310
次に、データ数と上位10名を見て見ましょう。
データ数は73名です。これは2018年に規定打席の1/3以上打席に立った打者の数になります。
柳田選手が1番で、満遍なく各チームからランクインしているように見えます。
> length(batter_18$出塁率)
[1] 73
> head(batter_18[c(2,3,17)], 10)
選手名 チーム 出塁率
1 柳田 悠岐 S 0.431
2 秋山 翔吾 L 0.403
3 近藤 健介 F 0.427
4 吉田 正尚 Bs 0.403
5 牧原 大成 S 0.341
6 浅村 栄斗 L 0.383
7 西野 真弘 Bs 0.333
8 中村 晃 S 0.369
9 井上 晴哉 M 0.374
10 島内 宏明 E 0.373
最後に箱ひげ図で視覚的に確認します。
> boxplot(batter_18$出塁率~batter_18$チーム, main="2018_BP")
箱ひげ図は、真ん中の太い線が中央値、実戦の箱の上側が第一四分位(上位25%の境目)、実戦の箱の下側が第三四分位(下位25%の境目)になります。
西武打線は上位4分の3が全体平均である0.32を超えており、他の球団に比べて高そう気がしますね。
概要を掴んだところで、早速検定を行なっていきましょう。
1. ある事象について、検定したい仮説(帰無仮説)を決める
まずは帰無仮説を考えて見ましょう。
帰無仮説は棄却したいこと、を設定します。
今回は西武が他の球団と比べて出塁率が高いということを確認したいので、否定する内容としては、実際は西武打線の出塁率は他の球団と同じである、という内容になります。
考え方としては、西武打線の出塁率の高さは、たまたま上振れただけなのか、それとも他の球団の選手と実力の違いが反映された結果なのかを確認します。
つまり、"たまたま上振れた"ということが、現実的に起こりうるのかどうか、です。
2. 仮説を検定するための検定統計量を選択する
西武打線の出塁率の平均と、パリーグ全体の出塁率の平均を比較します。
そのため、検定統計量(検定に使用する標本統計量)は以下になります。
・・・標本データの平均(西武の出塁率の平均)
・・・母集団データの平均(パリーグ全体の出塁率)
・・・標本データの標準偏差。不偏標準偏差を使用します。
・・・標本データのサンプル数
(補足)なぜt検定の検定統計量は上記の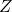
を用いるのか
そもそも、上記のZは何を求めているかというと、標本データの平均値を標準化した値になります。
※標準化については【標準化について】もご参考ください
標準化により、データの絶対量の違いの影響を受けずに、"検定値"に乗っ取って検定ができるようになります。
このことは、例えば同じ長さのデータをkmとmで分散を求めてみると理解できるかと思います。
3. 検定の判断基準(有意水準)を設定する(現実的に起こりうるものかどうかの基準)
厳密さが必要な場合は1%とすることもありますが、今回は5%とします。
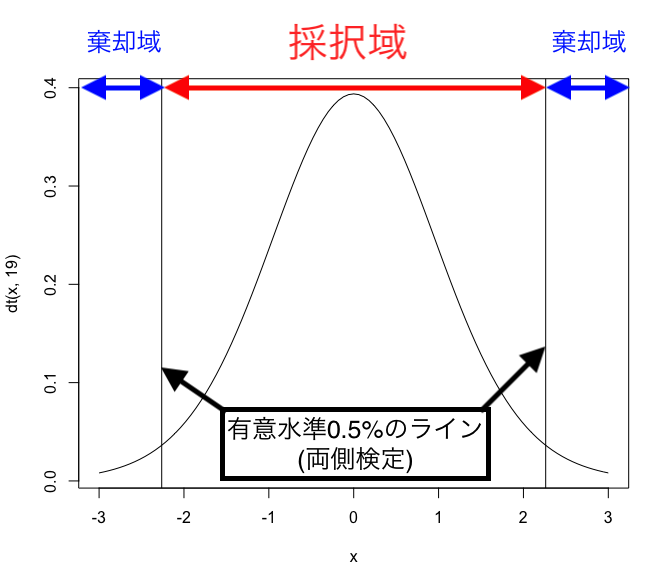
今回は"異常値かどうか"を確認したいため、両側検定とします。
("高いかどうか"or"低いかどうか"を検定する場合は片側検定となります。)
4. 今回の事象に対する検定統計量を計算(実現値)し有意水準と比較することで、仮説の正否(採用か棄却か)を判断する。
実現値の計算
条件が全て出揃ったので、実現値を計算します。
> X_bar <- mean(batter_18[batter_18$チーム=="L",]$出塁率)
> X_bar #標本データ(西武の打者)の平均出塁率
[1] 0.3518
>
> mu <- mean(batter_18$出塁率)
> mu #母集団の平均出塁率
[1] 0.3228356
>
> sigma_hat <- sd(batter_18[batter_18$チーム=="L",]$出塁率)
> sigma_hat #標本データ(西武の打者)の出塁率の不偏標準偏差
[1] 0.039589
>
> n <- length(batter_18[batter_18$チーム=="L",]$出塁率)
> n #標本データ(西武の打者)の数
[1] 10
以上で、検定統計量Zを求めるのに必要な値が導出できたので、Zを計算します。
> Z_value <- (X_bar - mu)/(sigma_hat/sqrt(n)) > Z_value
[1] 2.313608
この値を、有意水準5%で見たときのt検定値と比較します。
自由度の計算
ここで自由度(df)について確認する必要があります。
単独統計量におけるt検定の場合、自由度は標本データ数-1 となります。
今回は"標本データ数"は上記のnとなりますので、df=10-1=9となります。
仮説の棄却または採択の決定
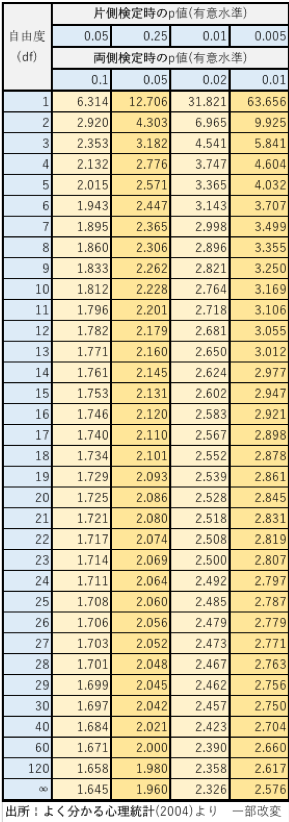
5章に記載したt分布表で、以下の条件に会う値を探します。
- 検定方法・・・両側検定
- 有意水準・・・5%
- 自由度・・・9
すると、"2.262"という値が出てきます。
これを先ほどの実現値と比較すると、実現値>t値となるため、今回の帰無仮説は棄却されます。
つまり、西武打線の出塁率は、たまたま高かったわけではなく、有意に高いということがわかりました。
(コラム)棄却と採択の意味について
これを視覚的に表すと以下になります。
このグラフにおいて、自由度等から求めたt検定の値2.262というのが"有意水準5%のライン"です。
そして、今回の実現値が2.313であり、下記の"棄却域"に入っていることがわかります。
これはつまり、
棄却域に入る=帰無仮説が棄却される=平均値に有意な差がある
となります。
４. t検定のための関数(R)
Rでは様々な関数が用意されており、その中にt検定のためのものもあります。
今回はその中で以下の３つをご紹介します。
- t値を求める方法
- p値(有意水準)を求める方法
- t検定を瞬時に行う方法
t値を求める方法(qt関数)
t値は、以下のように求めることができます。
t値 = qt(<<有意水準>>, <<自由度>>[, lower.tail=FALSE] )
※ lower.tail=FALSEは上側確率を求める際に使用されます。
※ デフォルトは片側検定のため、両側検定の際は有意水準を半分にします。
実際に求めて見ます。
今回の例では有意水準5%, 両側検定、自由度が9となります。
> qt(0.025, 9)
[1] -2.262157
> qt(0.025, 9, lower.tail=FALSE)
[1] 2.262157
先程と同様の値が出力されることを確認できました。
p値(有意水準)を求める方法(pt関数)
続いてp値(有意水準)を求めます。
これは、先程は手動で"5%"と設定した値ですが、実際は何%なのかを計算できます。
つまり、以下を求めることができます。
5%以下の確率でしか起こらない場合を特異と設定したが、実際は何%の確率で発生するのか
求め方は以下になります。
p値 = pt(<<実現値>>, <<自由度>>)
※ lower.tail=FALSEは上側確率を求める際に使用されます。
※ デフォルトは片側検定のため、両側検定の際はp値を倍にします。
実際に求めて見ましょう。
今回は3章で求めた通り、実現値は2.313608、自由度は9、両側検定になります。
> pt(2.313608, 9, lower.tail=FALSE)*2
[1] 0.04596425
以上から、今回の事象は約4.6%の確率で発生するものであるということがわかりました。
先ほど求めた通り、事前に設定した有意水準の5%を切っていることがわかります。
t検定を瞬時に行う方法(t.test関数)
t.test関数を使用することで、t検定時に導出する色々な値を瞬時に計算できます。
使い方は以下になります。
> t.test(<<標本データ>>, mu=<<母平均>>[, conf.level=<<信頼区間>>)
※ 信頼区間のデフォルト値は95%
実際に求めて見ましょう。
標本データは"batter_18[batter_18$チーム=="L",]$出塁率"(batter_18に全チームのデータが入っており、そこからチーム列がLの行を抽出)。
母平均は"mean(batter_18$出塁率)"になります。
> t.test(batter_18[batter_18$チーム=="L",]$出塁率, mu=mean(batter_18$出塁率))
One Sample t-test
data: batter_18[batter_18$チーム == "L", ]$出塁率
t = 2.3136, df = 9, p-value = 0.04596
alternative hypothesis: true mean is not equal to 0.3228356
95 percent confidence interval:
0.3234797 0.3801203
sample estimates:
mean of x
0.3518
出力の3行目の以下では、順番にt値(実現値)、自由度、実現値のp値(先ほどpt関数で求めた値)が出力されています。
このように、先ほど苦労して求めた値を一瞬で求めることができました。
この結果からも、p-valueは0.046であり今回設定した有意水準5%より低いため、帰無仮説は棄却できるという結論を導けますね。
t = 2.3136, df = 9, p-value = 0.04596
なお、出力5行目の"95 percent confidence interval:"は信頼区間における信頼係数を表示しています。
今回はこちらの詳細は省きます。
5. (参考) t分布表とその使い方
t検定を行う際に使用するt分布表です。
使い方は自由度と、使用した検定方法とp値の二つが交わるところの値がt値となります。
例えば、自由度10で片側検定で、p値を0.05(5%)とした場合、t値は1.812となります。
このt値が求めた実現値より大きければ帰無仮説は棄却されます。
